混合模型框架下的模型,如潛變量增長混合模型(latent growth mixture modeling,LGMM)或潛類別增長分析(latent class growth analysis,LCGA),因估算過程中涉及多個決策過程,導致潛變量軌跡分析結果的報告呈現多樣性。為解決這一問題,指南制訂小組按照系統化的制訂流程,通過 4 輪德爾菲法調查,遵循專家小組意見,提出了各領域報告潛變量軌跡分析結果時需采用統一的標準,最終確定了報告軌跡研究結果必要的關鍵條目,發布了潛變量軌跡研究報告規范(guidelines for reporting on latent trajectory studies,GRoLTS),并利用 GRoLTS 評價了 38 篇使用 LGMM 或 LCGA 研究創傷后應激軌跡的論文的報告情況。
估計潛變量軌跡的研究方法在社會學、行為學和生物醫學領域越來越流行[1-3]。因其在混合模型框架下進行模型估計的過程中會涉及多個決策過程,選擇不同的決策方案會在一定程度上影響研究結果,甚至可能產生不同結論。盡管目前潛變量軌跡分析十分受歡迎,并成為了許多領域內分析縱向數據的主流工具,但尚無潛變量軌跡模型結果的報告標準。這導致了論文中對潛變量軌跡分析結果的報告存在很大差異,而不充分或不完整報告潛變量軌跡分析結果會妨礙對結果的解讀和批判性評價,并且影響不同研究間結果的橫向比較。
本文介紹潛變量軌跡研究報告規范(guidelines for reporting on latent trajectory studies,GRoLTS)。GRoLTS 的最終目標是提高潛變量軌跡研究報告的一致性,使研究結果可完全透明(高質量)地呈現,并且可用于研究間的比較、重復、系統評價和 Meta 分析等。在本文中,我們將首先描述 GRoLTS 的制訂過程,即采用系統化的制訂過程,通過 4 輪德爾菲法,由專家小組確定報告軌跡研究結果必要的關鍵條目;隨后詳細描述每一個關鍵條目內容;最后,介紹利用 GRoLTS 評估 38 篇使用潛變量軌跡分析探討創傷后應激癥狀(posttraumatic stress symptoms,PTSS)變化研究的報告情況。更多相關信息請參閱 Open Science Framework(https://osf.io/vw3t7/),包括:① 德爾菲研究的全部細節;② 可用于教學的部分條目的補充信息;③ 篩選 38 篇 PTSS 論文的數據集。
1 GRoLTS 的制訂
GRoLTS 的制訂過程包括以下階段[4]:① 初步確定主題;② 形成條目;③ 評估表面效度;④ 評估一致性和結構效度的現場試驗(field trials);⑤ 制訂最終的精煉條目清單。
指南制訂之初,制訂小組明確了 GRoLTS 需符合以下基本要求:① 適用對象為探索性使用潛變量軌跡分析來回答實質研究問題的論文;② 總結報告潛變量軌跡分析結果的要求;③ 確保不同背景的研究人員能夠一致、可靠地使用此報告規范進行報告;④ 條目簡明扼要易于完成,同時應包括確保結果可重復性和透明性的所有方面。
在制訂階段,制訂小組共邀請 27 名專家(參見致謝中的專家名單),并向他們提供了 GRoLTS 的制訂目標和要求,通過前 3 輪德爾菲法和第 4 輪現場試驗評估所有條目的表面效度。制訂小組采用德爾菲法在專家小組中就 GRoLTS 應包括哪些標準及具體條目的措辭達成一致。以上每個步驟的具體細節,包括 GRoLTS 的所有前期版本請參閱 Open Science Framework(https://osf.io/vw3t7/)。
2 GRoLTS 條目和解讀
GRoLTS 包含 16 個條目(部分含子條目,表 1)。每個條目評分為 0(未報告)或 1(已報告)。建議在如下情況使用 GRoLTS:① 研究人員準備提交論文前;② 編輯、審稿人和授權專家核查論文是否報告了所有基本要素;③ 老師向學生講解潛變量軌跡分析結果中哪些要素是重要的。我們將對每一個條目(特別是復雜的條目)進行解讀,并對文獻中討論內容進行概述。關于條目 1、2、7 和 14 的更詳細信息請參閱 Open Science Framework(https://osf.io/vw3t7/)。
條目 1:是否報告統計模型中所使用的時間度量?
在任何類型的增長模型中,時間編碼對結果解讀都具有重要意義。如 Eggleston 等[5]研究所示,隨訪時間長度會影響潛變量軌跡的數量,形狀-時間越長,軌跡越多。此外,Piquero[6]對基于犯罪數據的潛變量增長混合模型(latent growth mixture modeling,LGMM)和潛類別增長分析(latent class growth analysis,LCGA)進行系統評價后發現,時間點的間隔也會影響軌跡數量。因此,不僅要透明地報告時間度量,更要正確地設定時間點間隔。時間度量的設定應該在分析開始前依據研究設計確定,而非根據模型的擬合程度或增長參數的顯著性。關于時間度量更深入的討論請參閱 Open Science Framework(https://osf.io/vw3t7/),及 Biesanz 等[7]或 Duncan 等[8]的研究。
條目 2:是否提供單個隨訪的均數和標準差?
在縱向研究中,由于組織安排的原因,對不同研究對象進行多次數據采集時,不同個體間的采集時間間隔必然存在一些差異。這種差異被稱為時間-非結構化數據或隨訪內變異。與之相對應的是時間-結構化研究,即所有研究對象的數據均以相同的時間間隔采集。在某種程度上,絕大多數縱向數據是時間-非結構化的。也就是說,并非所有研究對象都在相同的時間點采集數據,請參閱 Palardy 等[9]的實例。然而,時間-非結構化數據往往會被研究者忽略時間的非結構化特性,而按照時間-結構化數據進行分析,這可能嚴重曲解分析結果真實性。Singer 等[10]發現,當使用預期年齡而非實際年齡作為時間度量時,會高估線性斜率、截距和線性斜率的方差。Mehta 等[11]、Hertzog 等[12]及其他幾個模擬研究[13,14]也得出相似的結論。我們建議,在每個數據集中納入一個時間變量,用于記錄不同觀測點間的確切時間間隔,以便能夠在方法部分計算并報告時間間隔的變異程度。因此,可使用隨個體觀測時間變化的隨機因子載荷替代固定因子載荷(更多細節請參閱 Coulombe 等[14])。更詳細的解釋和圖解說明請參閱 Open Science Framework(https://osf.io/vw3t7/)。
條目 3a:是否報告缺失數據機制?
大多數縱向研究存在缺失數據或研究對象失訪問題。在描述缺失數據和失訪情況時,應首先報告數據缺失機制。數據缺失機制一般可分為三種類型[15]:① 完全隨機缺失(missing completely at random,MCAR),即所有缺失數據的發生不依賴于所有觀測到或未觀測到的變量;② 隨機缺失(missing at random,MAR),即缺失數據可能依賴于觀測到的變量,但不依賴于未觀測到的變量;③ 非隨機缺失(missing not at random,MNAR),即缺失數據依賴于未觀測到的變量。我們無法判斷數據缺失屬于 MAR 還是 MNAR(因無法檢驗),只能盡量保證數據的缺失符合 MAR 假設。統計模型如 LGMM/LCGA 的假設均基于 MAR。因為對所有研究對象均進行了多次測量,只要失訪不是以某種特定方式系統性地發生,在縱向隊列中就可假定該失訪滿足 MAR 情況(即這些個體的觀測變量得分的缺失,可假定是隨機的)。
條目 3b:是否描述與失訪或缺失數據相關的變量?
正如 Asendorpf 等[16]的研究所示,對于縱向研究,即使每一輪隨訪中微小且不顯著的選擇性退出,效應也會在整個隨訪過程中逐漸累積,最終導致結果產生越來越大的偏倚[17]。因此,研究者應比較退出與完成研究的對象的相關特征。與失訪或缺失相關的變量(也稱輔助變量)可作為模型中的協變量(服從 MAR 假設下擬合)或可在多重填補(multiple imputation,MI)模型中使用。使用 MI 的優點是可將缺失數據的處理與目標模型區分開來。
條目 3c:是否描述分析過程中缺失數據的處理?
關于缺失數據報告的第三個問題是在分析過程中如何處理缺失數據。在許多論文中都引用了 Peeters 等[18]對不同填補模型的比較。目前,處理缺失數據較為普遍和靈活的方法是利用鏈式方程的多重填補(也稱預測均值匹配)[19,20]。
條目 4:是否納入觀測變量分布類型的信息?
潛變量軌跡分析中的因變量可存在不同形式。通常假設變量是連續型且在組內呈正態分布,但實際上并非總是如此。因變量可能不是連續型變量,而是分類變量(如,具有五個應答類別的李克特式量表)、計數資料(如,計數某人的癥狀數量)或零膨脹型(如,80%~90%的研究對象得分為 0)。正如 Vermunt[21]所述,假設組內因變量呈正態分布至關重要,當假設因變量在組內呈多項分布(非正態分布)時,建議不使用連續型變量混合模型,應轉而使用離散型變量混合模型。Bauer 等[22-24]研究發現,當變量分布的假設不成立時(即當實際的結局分布為非正態分布時),即使結果只呈現一組軌跡[25]也更傾向于選用多軌跡群組模型,只要在統計分析軟件中設定研究結局的類型,潛變量軌跡框架就可輕松處理該類變量,并避免過度提取潛類別。另一種方法是使用潛變量[26],即通過使用單個條目分數而非總分來考量結局的測量結構。如果模型中的潛變量有意義,那么潛變量和調查條目的測量結構應該隨時間穩定,即測量結構不隨時間變化而變化。以上是一個需要檢驗的重要假設,又被稱為測量不變性[27],雖然該假設并不總是成立,但該假設會對結果產生較大影響[28]。
條目 5:是否提及統計分析軟件?
目前可用于估計潛變量軌跡的程序包有以下幾種:LatentGold[29]、Mplus[30]、SAS Proc Traj[31]、Stata GLLAMM[32]、R 程序包 LCMM[33]、R 程序包 OpenMx[34]等。這些程序包指定默認模型的方法均有所不同。例如,Mplus 的默認設置是在組間限制協方差和(殘差)方差。相反,在 LatentGold 中則使用先驗殘差進行后驗方法估計,以防止殘差變為 0。出于可重復性的考慮,提供使用的軟件及版本信息至關重要(因為版本更新可能涉及到后臺算法調整)。在下一個條目中,我們會進一步討論方差-協方差矩陣的設定。
條目 6a:是否考慮并清晰記錄處理組內異質性的方式(如 LCGA 或 LGMM)?
在建立潛變量軌跡模型時,為精確地指定模型需要做許多選擇。處理組內異質性的第一種方法,涉及潛類別內增長參數的方差。有兩種潛變量增長模型可解釋未觀測到的群體。如果在潛變量軌跡內估計增長參數的方差,則這種建模靈活性稱為 LGMM[1,35-38]。如果假設組內所有個體增長軌跡是同質的,且假設組內增長因子的方差和協方差估計值固定為 0,則稱為 LCGA[39-42]。Groudace[43]、Erosheva[44]、Feldman[45]、Jung[46],Kreuter[47]和 Twisk 等[48]很好地總結了 LGMM 和 LCGA 間的區別。
Nagin[39,41]運用理論方法并引入潛變量軌跡模型的兩個概念:① 作為群體異質性連續但未知分布的近似值;② 作為具體的軌跡,可視為非常重要的實體。在第二種概念中,該軌跡有描述性名稱,并作為不同的實體進行討論。Erosheva 等[49]的系統評價表明,大多數研究人員采用第二種方法(第 325~326 頁),但能夠真正發現不同軌跡組別的情況其實十分罕見。正如參與本指南解讀的一位專家所說:“我還沒遇到過一種能夠明確表述的發展理論,它能先驗地參數化增長因子組內方差-協方差的結構。”Twisk 等[48]認為應從可行性角度出發選擇研究方法。由于 LGMM 算法較難,研究人員常選用 LCGA。但實際上 LGMM 更靈活,因為該方法考慮了前面提到的組內變異帶來的異質性問題,但這種靈活性也帶來了一定的問題:如需要更強的計算能力、需要更大樣本量、可能引發收斂問題等。既往在專業期刊如Infant Child Development上,已對使用何種參數化方法這一問題進行了激烈討論[25,37,50,51]。本文對這一問題不再贅述,只強調應在論文中討論最終模型的選擇。理想情況下,應采用兩種模型擬合數據并進行比較。提出此建議的原因是實際結果會因模型選擇的不同而異,因此檢查每種方法對于理解其對最終模型解釋的影響非常重要。
條目 6b:是否考慮并清晰記錄處理組間方差-協方差矩陣結構差異的方式?
除 LGCA 和 LGMM 間的差異外,第二個問題是約束誤差結構(相較于不同類別中自由估計)。約束誤差結構與不同類別間增長因子方差-協方差矩陣的異質性(相較于同質性)相互影響。也就是說,潛類別間的殘差和方差-協方差矩陣是相同的,還是不同的?以下原因可解釋為什么殘差在潛類別間保持不變或各潛類別具有特定的殘差:潛類別間殘差相同是以偏離增長曲線的變異在組間沒有差異為假設,而潛類別間殘差不同則是以某些組(這里指潛類別)偏離增長曲線的變異要大于其他組為假設。組內特定的殘差可能更符合實際情況,然而由于模型包含多項參數,因此該情況可能引發估計問題。此外,若使用連續數據模型分析離散數據,則會出現殘差為零的情況。我們建議研究人員應基于已知、具體的信息及分析過程中出現的估算問題選擇相應模型。
是否約束潛類別間方差-協方差矩陣更需要考慮現實問題。雖然每個潛類別都允許存在特定的方差-協方差矩陣,但由于模型需要估計大量參數,因此需要更大的樣本量來避免收斂問題。對于較小樣本量的解決方法是分別估計方差-協方差矩陣,研究人員多采用約束方差-協方差矩陣來簡化模型(或處理局部極大值的誤差信息)。無論采用何種方法設定組間方差-協方差矩陣,研究人員都應在論文中明確報告,因為不同設定均會對研究結論產生實質性影響。具體來說,研究人員應盡可能清楚地列出所有使用的研究方法及原因(如,“理論表明增長因子的變異在亞組間是恒定的,因此我們認為矩陣相同”等)。其次,研究人員應根據所作假設解釋結果。需注意的是,若重新定義方差-協方差矩陣,結果也可能隨之改變。例如,如果協方差矩陣改變(如各類別間自由估計),則潛類別的估計結果也會隨之改變并產生完全不同的解釋。
條目 7:是否描述軌跡的形狀和函數形式的設定?
令趨勢線變化的主要方法之一是指定用于捕獲隨時間變化的增長函數。基于多項式函數的增長模型通常用于估計線性、二次、三次等變化[38]。然而,增長不需要通過多項式函數估計。許多非線性參數模型也常用于估計增長,例如 logistic、Gompertz 和 Richards 增長曲線[52]。平滑函數的半參數模型,如廣義加性模型,同樣可用于估計增長[53];此外,還可使用分段模型[9,54]。我們建議不僅要報告每條軌跡在最終模型中的形狀,還需要根據指定函數驗證模型:例如,比較線性增長模型與包含二次效應模型的結果。關于不同形式的增長函數是如何影響增長參數解釋的問題,請參閱 Open Science Framework(https://osf.io/vw3t7/)。
條目 8:如果納入協變量,分析是否仍可重復?
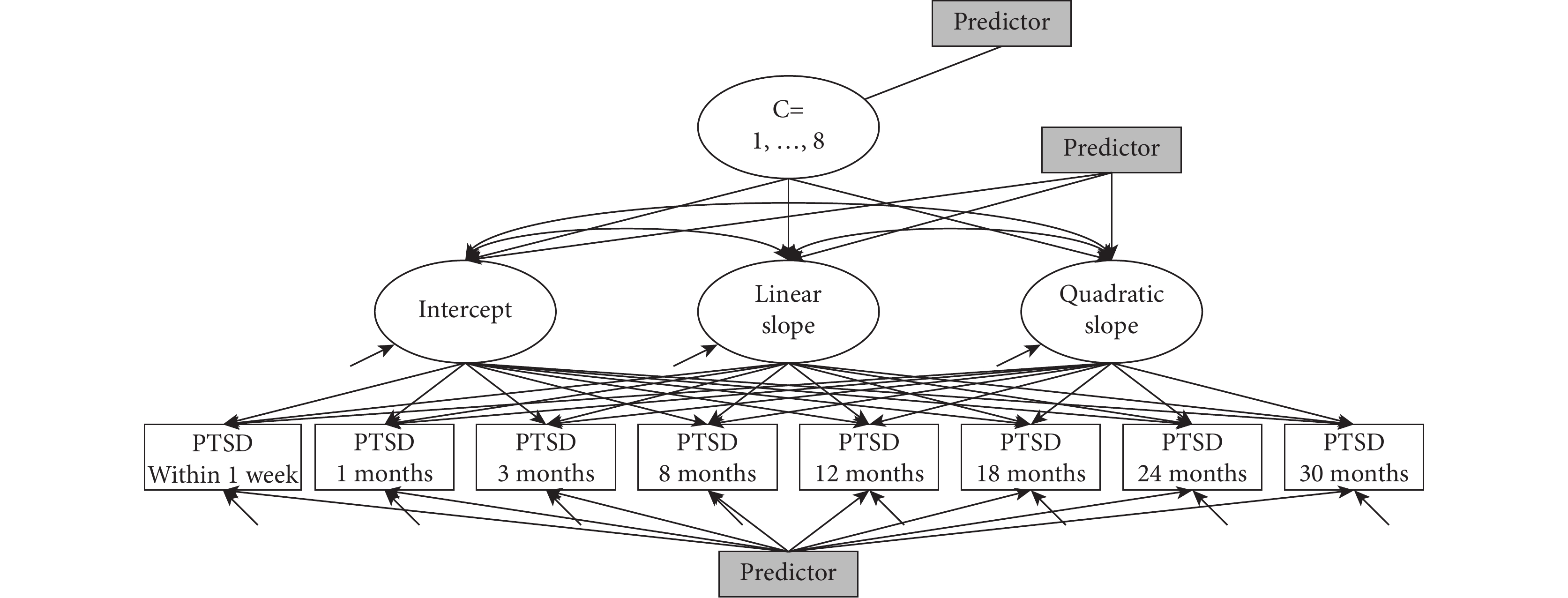
預測因素(或協變量)可在 3 個不同水平添加到模型中(圖 1):① 在因變量水平上作為依時或非依時協變量納入,以控制在特定時間點的變異;② 在增長參數水平上納入,以尋找不能通過協變量個體差異(如年齡、膳食、社會經濟狀況)解釋的潛類別;③ 在自變量水平納入,以預測潛分組。如果協變量被指定為模型的一部分,那么該模型通常被稱為條件模型;而非條件模型是指在忽略協變量的情況下探索潛類別數量。需注意的是,無論預測因素出現在模型中的哪個位置,它們既可是直接觀測到的變量也可是潛變量。目前有多種方法可用于預測潛分組,我們將在下文逐一介紹。
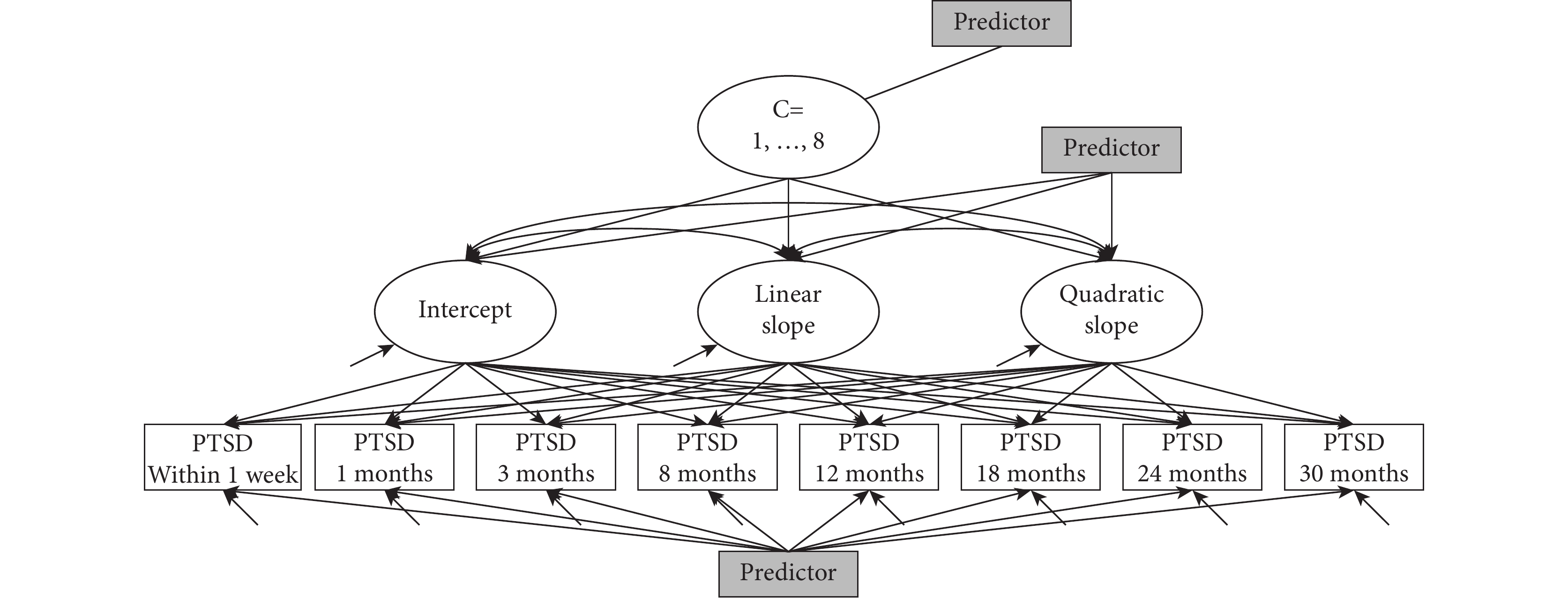 圖1
潛變量軌跡分析模型示例
圖1
潛變量軌跡分析模型示例
該模型包括 1~8 個類別(C=1,…,8),8 個重復測量變量(創傷后應激障礙,posttraumatic stress disorder,PTSD 等),3 個增長參數(截距、斜率、二次項)和可添加協變量的 3 個位置。
一步法:在聯合模型中可納入潛分組的預測因素,該模型可同時估計組別和預測潛分組。一步法有兩個缺點:第一,納入的預測因素可能會不適當地修改潛類別結構的構成。理論上,模型中的任何改動都會影響潛類別下個體的劃分。由于協變量會影響潛類別的形成,所以在模型中直接加入預測因素會導致結果的缺陷。此外,因為潛變量是通過測量指示變量獲得,直接加入預測因素可能使潛類別失去意義(第 329 頁)[55]。La Greca 等[56]詳細描述了這種效應(第 360 頁)。在這種特定情況下,應重新考慮潛類別數量,而不是繼續采用在沒有納入協變量的情況下所確定的類別數量。無論改變潛類別估計結果的效應是否對研究人員有意義,對于在模型中納入或不納入協變量的標準仍不明確;參閱 Palardy 等[9]的研究,其根據所需的潛類別數量比較了有、無協變量模型的區別。總之,希望研究人員不要將選擇主要預測因素的問題與發現潛類別數量的問題混為一談。第二,受影響的還有一個稱為熵的指數(另見條目 13)。熵的作用是評價將個體劃入各潛類別這一分類過程的準確性,反映了根據個體軌跡和協變量值預測潛分組的水平。若熵值接近 1.0,則認為進行了適當的分類;若熵值接近 0,則認為分類效果較差。采用人工納入預測因素的一步法會人為地高估熵指數,導致過于夸大分類的可信度。而且,熵本身的含義也在變化。
標準三步法:保留最合適的潛分組并分別分析數據 按照該策略,首先在沒有潛分組預測因素的情況下確定潛類別的數量(步驟 1)。隨后保留最合適的潛分組與原始數據合并(步驟 2),并采用多項式回歸分析將其與潛變量軌跡模型分開分析(步驟 3)。Andersen 等[57](補充材料,第 2 頁)和 Pietrzak 等[20](第 208 頁)清晰描述了該方法。盡管該方法采用了最合適的潛分組策略來解決了一步法存在的各種問題,但它忽略了潛類別分配的不確定性。換句話說,該策略假設個體在潛類別分配中不存在錯分。其結果是,基于協變量的預測可能低估真實效應。但是可通過熵來評估低估程度:熵值越高,錯分越少,潛分組預測結果偏倚越小[58]。保留最合適的潛分組策略要求熵值足夠高,且作者承認衰減效應。
使用“偽分類”方法的三步法:由 Wang 等[59]提出的方法是:首先估計潛類別模型,然后基于從模型中獲得的后驗分布采用 MI 處理潛類別變量,隨后使用由 Rubin 等[60,61]提出的 MI 技術,分析填補的潛類別變量和協變量。Peutere 等[62](第 17 頁)詳細地描述了該策略。與前文提及的其他方法相同,若使用偽分類方法,研究人員應進行明確地描述,并且說明潛類別變量是通過 MI 獲得。
調整錯分三步法:該方法由 Vermunt[3,63]在 Bolck 等[64,65]的思想上發展而來。與前文中的三步法不同,該方法考慮了第三步分析中潛類別分配下的錯分問題,即估計所得潛分組并非真實的潛分組這一問題。實際上,估計潛類別模型,只是將步驟 2 中指定的潛分組作為單一指示變量,根據步驟 1 和 2 的估計值確定錯分概率(第 330 頁)[55]。該方法允許協變量在標準潛類別模型中預測潛分組,但也可通過潛分組預測遠端結局[66]。
調整錯分三步法與前文中提及的三步法具有相同的優點,即可將構建對目標響應變量有意義的潛變量軌跡模型與構建探究潛類別與外部變量關系的模型區分開來。但需注意,該方法同樣存在前提假設,除了要求外部變量和潛類別指示變量相互獨立之外,當外部變量為遠端結局時,還需正確設定遠端結局的組間分布。請注意,盡管可放寬條件獨立假設,但該假設同樣適用于一步法。針對遠端結局組間分布,Bakk 等[66]表示,即使偏離分布假設,BCH 變異[64]仍然穩定,但最大似然(maximum likelihood,ML)變異卻并不穩定。
總之,可在 LGMM 中的 3 個不同水平納入協變量(圖 1),并且當分析目標是預測潛分組時,至少有 4 種納入協變量的方法,同時也是納入協變量的常見原因。由于納入協變量的方式和方法對模型結果解釋有很大影響,在沒有明確推薦方法的情況下,作者對上述過程進行完全透明的報告極為重要。
條目 9:是否報告隨機起始值數量和最終迭代次數?
若使用 ML 估計潛變量軌跡模型,了解最終的潛類別估計結果是否已收斂到 ML 分布的最大值而不是所謂的局部最大值十分重要。因為 ML 函數有時不僅只有一個最大值,還可能存在幾個最大值,這種情況需要根據模型參數的起始值找到“真實”(即絕對)的最大值。因基于局部最大值(相較于真實最大值)的估計結果可能與最優結果有很大不同,所以強烈建議基于多個不同起始值重新運行模型,以確保找到最優解。在統計學文獻中已經非常詳細地討論了在估計混合模型時使用多組起始值的重要性。例如,Hipp 等[67]詳細討論了不恰當或起始值過少對結果的影響。研究發現,當起始值錯誤時估計結果可能有實質性的錯誤。每個估計的參數都有相對應的較為適當的參數空間,他們建議根據這些空間“明智地”確定每個參數的起始值。參數的起始值可隨機生成,但是在混合建模環境中,通常基于某些理論選擇這些參數。Finch 等[68]討論了基于某理論在潛類別分析中選擇閾值起始值以避免在錯誤的參數空間中探索估計算法的問題。此外,為充分探索參數空間并避免僅收斂到局部最大值,建議將每個參數的起始值數量增加到至少 50 到 100 組[67]。當研究人員基于某理論或既往研究設定起始值時,這些起始值集合包含了既往相關起始值的隨機波動,可確保所有集合覆蓋了可能的參數空間。
條目 10:是否從統計的角度描述模型比較(和選擇)工具?
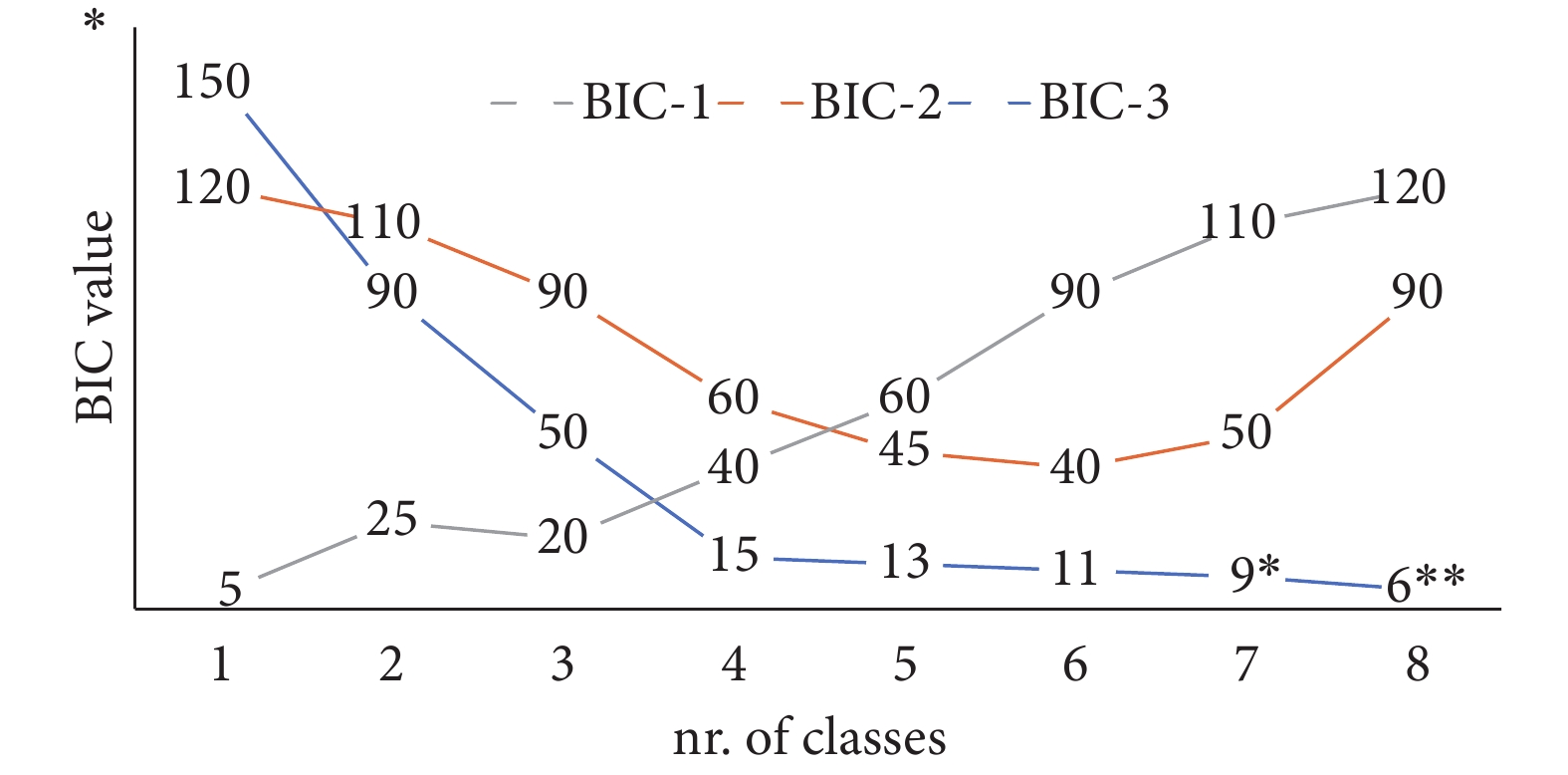
多項統計標準可用于判斷模型對數據的擬合程度,即應當劃分出多少潛類別。Nylund 等[69]的大樣本模擬研究顯示,貝葉斯信息準則(Bayesian information criterion,BIC;Schwarz[70])的表現優于其他模型選擇工具如 LGMMs 背景下的 Akaike 信息準則(Akaike information criterion,AIC)[71]。兩者都是基于對數似然把參數數量作為模型復雜性的懲罰項,以此來評估相對模型充分性的模型選擇工具。從軌跡數量的角度來看,具有最小 BIC 值的模型最優(參見圖 2 中模型 2 的結果)。BIC 目前已有許多衍生形式,其中樣本量調整的 BIC 有時也用于潛變量軌跡研究。
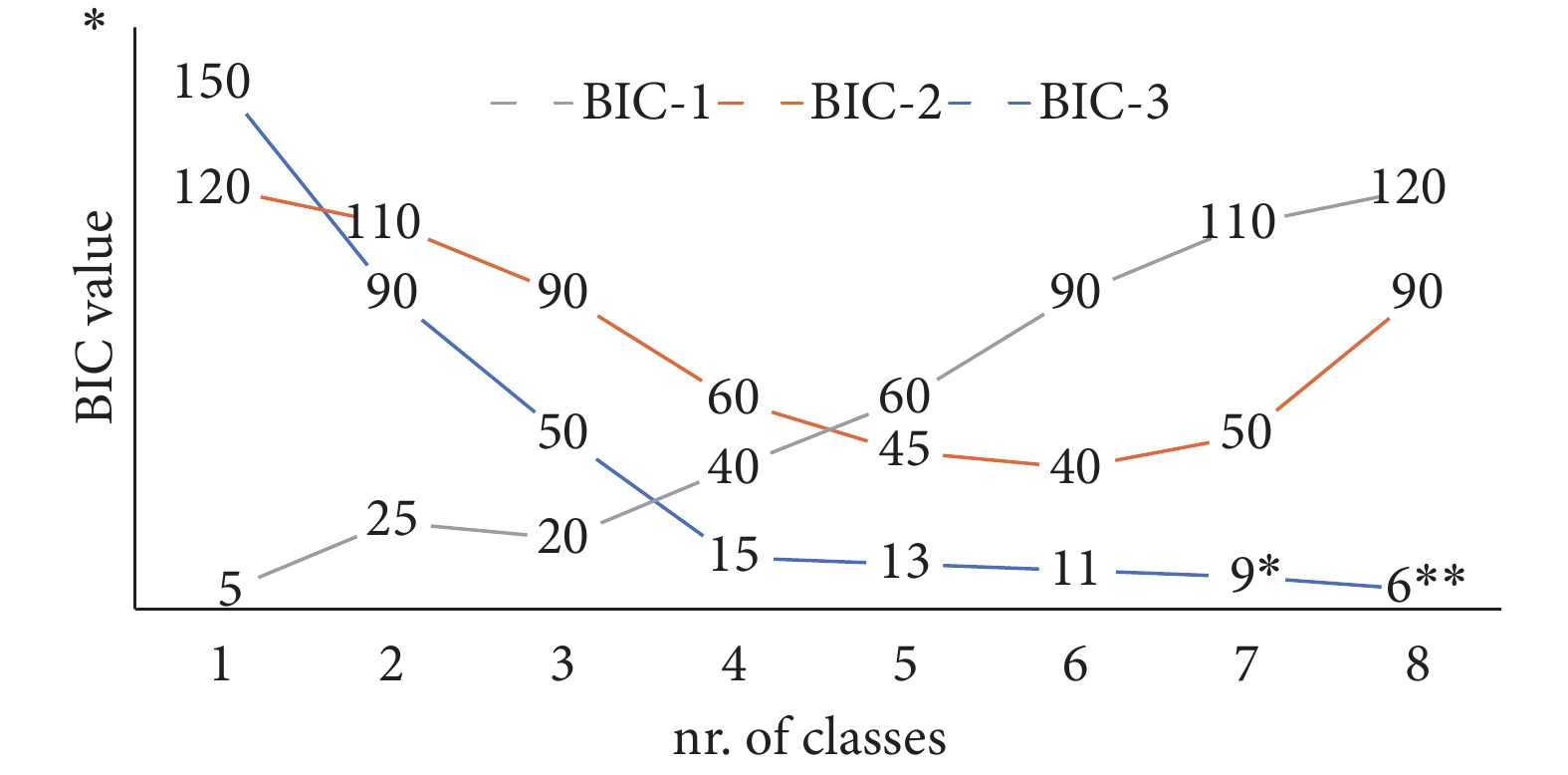 圖2
比較三個假設模型的貝葉斯信息準則值(BIC-1,BIC-2,BIC-3)
圖2
比較三個假設模型的貝葉斯信息準則值(BIC-1,BIC-2,BIC-3)
需注意,帶有一個星號的模型表示隨機啟動次數增加到 1 000,帶有兩個星號的模型沒有達到收斂。
由 Lo 等[72]提出的 Lo-Mendel-Rubin 似然比檢驗(Lo-Mendel-Rubin-likelihood ratio test,LMR-LRT)是另一種常用的模型選擇工具。LMR-LRT 檢驗k?1 個類別是否優于k個類別,若檢驗結果顯著,則表明拒絕k?1 個類別的零假設,接受至少k個類別。但 Jeffries[73](第 901 頁)指出,“該方法還未得到證實,模擬研究表明其結果可能不正確。”隨后,Nylund 等[69](第 538 頁)回應,最初在 Lo 等[72]的早期模擬研究表明,盡管如 Jeffries 所述,可能存在分析不一致性,但 LMR-LRT 仍可作為一種用于類別算法的有效檢驗工具。鑒于既往文獻中潛在的不一致,我們建議研究人員不要僅根據 LMR-LRT 工具確定類別數量。最近,有模擬研究證明 bootstrap 似然比檢驗(bootstrap likelihood ratio test,BLRT)[74]是選擇最優類別數量的良好指標[69],當將其應用于經驗數據時總會得到顯著結果。
盡管就評估擬合程度的方法仍有諸多爭議,但專家小組已經達成共識,推薦使用 BIC。當模型選擇工具和熵指數所確定的最優維度很大、各工具評估結果相互沖突或與理論沖突時,研究人員在實際操作中常將潛變量軌跡的數量減少至理論上有意義的數量。例如,研究人員通常會刪除只有微小變異的軌跡(如,Galatzer-Levy 等[75])或拒絕有收斂問題的模型(如,Orcutt 等[76])。
總之,我們建議研究人員如實描述選擇最終模型的過程。基于現有文獻,我們建議選擇 BIC 作為模型比較工具,但也建議研究人員使用多個工具來避免“選擇性失明”(即只看到有利于結論的證據,忽略不利證據)。請參閱表 2 和圖 2,了解如何選擇并使用模型比較工具(請注意,表 2 采用模擬數據用以舉例說明)。如類似表 2 情況,擬合指數在最優類別數量上不一致,應告知這一結果。作者應報告所有檢驗的模型,并最好結合理論對最終所選模型舉例說明(另見條目 14)。值得注意的是,有研究提出了許多可供選擇的指標[59]且該領域正迅速發展[77],因此研究人員應該及時關注該領域的新進展。
條目 11:是否報告擬合模型總數,是否包括僅含一個類別的模型?
軌跡分析的目的是找到描述數據集變異的潛類別的最優數量。為了找到類別最優數量,我們建議采用先從僅含一個類別開始的前進建模法,這是擬合效果最好的非混合潛變量增長模型。該模型簡單地假設群體中不存在亞組,隨著時間的推移所有個體或多或少遵循相同的軌跡。研究人員通常不會報告僅含一個類別的結果,但往往非混合模型能更好地擬合數據。圖 2 中模型 1 所示,假如不報告僅含一個類別的結果,根據 BIC 的值會選擇含三個類別的模型。但當報告僅含一個類別的結果時,BIC 提示一類別為最優模型。在這種情況下,結論則應為群體中不存在潛類別(即一類別為最優)。在擬合一類別模型后,應該逐步增加類別以確定哪個模型擬合最好。當模型擬合指數不再優化時也不應停止此過程,應該繼續擬合至少一或兩個額外的模型,以確保所有可能的模型都納入了分析。
條目 12:是否報告每個模型下每組所含個體數量?
確定最終類別數量時不應僅基于統計標準。例如,統計上的最優解軌跡可能只含有非常少的研究對象。當兩個群組(即潛類別)的規模明顯不同時(如一個群組遠大于另一個),大的群組會覆蓋小的群組,從而導致對群組規模和相應增長軌跡的錯誤估計[78]。此外,由于缺乏足夠的實質性信息來識別群組,模型可能無法正確識別樣本量較小的群組。在此情況下,軌跡的識別可能基于異常值或其他隨機波動,而不是真實的群組[22,36,79]。因此,研究人員應提供每個模型中各潛類別下樣本量的相關信息(具體操作過程請參閱表 2)。
條目 13:如果軌跡分析的目的是對個體進行分類,是否報告熵?
對個體進行分類是潛變量軌跡研究的常見分析目的,在這種情況下,研究人員必須報告分類的性能。評價分類性能的工具之一是相對熵值,該值越高表示個體歸類越準確。也就是說,模型能夠清晰地對特定類別中的個體進行分類,并且不同類別間存在足夠的區分度[78]。相對熵也被稱為衍生潛類別的“模糊性”度量[80,81]。當每個研究對象的所有后驗概率相等時,相對熵值為 0(即在三個潛類別下,所有參與者被分到其中一個潛類別的后驗概率為 0.33)。當每個參與者僅完全適合一個潛類別時相對熵為最大值 1,表示潛類別間能完全區分開來。因此,當熵值過低時需要小心,這提示研究對象沒有很好地被分類或沒有被分配到合適的潛類別。綜上,Celeux 等[58]提出,相對熵可被視為評估潛變量軌跡模型劃分數據效能的度量,Greenbaum 等[82](第 233 頁)對此進行了更為完善的解釋。然而,相對熵并不適用于確定潛類別數量[80,83,84]。Ram 等[85]建議,在多個模型的擬合指數(如,BIC)近似時,較高熵才對模型選擇有意義。盡管如此,我們仍建議作者報告熵值(見表 2)或像 Greenbaum 等[82](第 233 頁)一樣報告每個模型中的錯分數量。
條目 14a:是否報告最終結果的估計平均軌跡圖?
條目 14b:是否報告每個模型的估計平均軌跡圖?
如前所述,許多研究人員單獨使用實質性論據或結合模型選擇工具來決定潛類別數量。檢查軌跡圖對評估不同潛類別估計結果下的模型效能十分有幫助。需要報告的第一類圖為平均軌跡,不僅局限于最終模型,而應覆蓋所研究的每個模型(如在建模和評估分析結果階段均應進行模型比較)。我們在 https://osf.io/vw3t7/中提供了一個示例。因可能有大量模型需要擬合,報告全部軌跡圖存在一定挑戰性,但如果僅根據理論論證來決定類別數量,則必須報告所有估計結果的軌跡圖。需注意的是,若期刊不允許在正文中呈現較多的圖,可將該信息作為在線補充材料。我們認為,必須提供完整的軌跡圖信息以便其他研究者可重現最終分類數量。
條目 14c:是否報告最終模型的估計均值和每個潛類別下實際觀測到的個體軌跡圖?
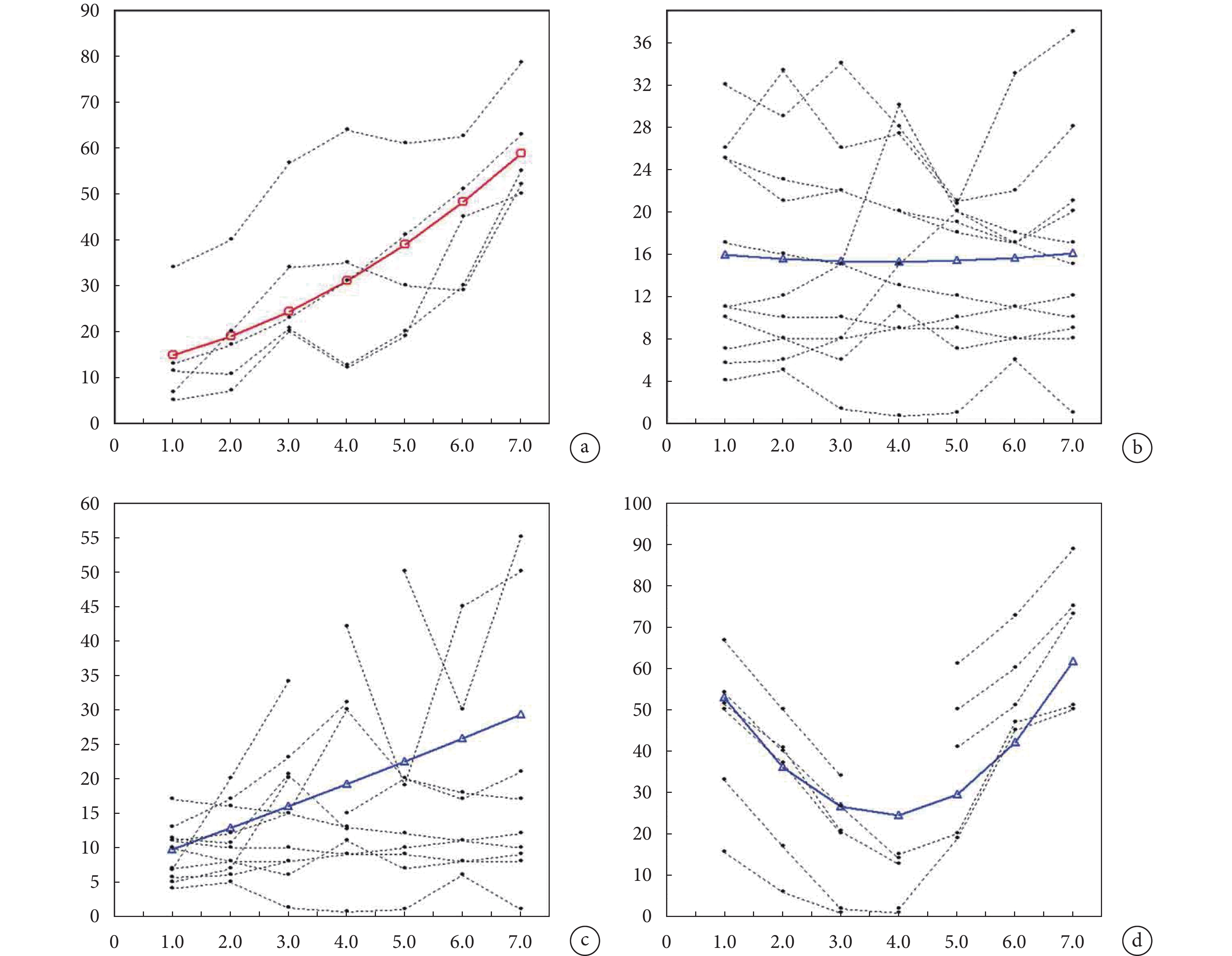
除報告每個模型的估計平均軌跡外,結合實際觀測到的個體軌跡分析最終估計平均軌跡也十分重要。Erosheva 等[44]提出,通過上述圖示可直觀地看到潛變量群體軌跡對個體差異的解釋程度,及不同組別下實際觀測到的個體重疊程度。如圖 3 所示,所有個體可能都遵循平均軌跡且可能采用了 LCGA(圖 3a)。需注意,盡管該圖展示了個體軌跡的變化,但隨時間推移它們基本上都遵循相同的增長模式。但圖 3b 中個體軌跡差異較大,平均軌跡并未反映數據的真實情況。圖 3c 中,實際上沒有一個個體軌跡遵循平均軌跡,那么即使有足夠的擬合統計量,對結果的可解釋性也存在一定質疑。圖 3d 的情況更不理想,因為其中的二次效應完全可能是缺失數據所致。
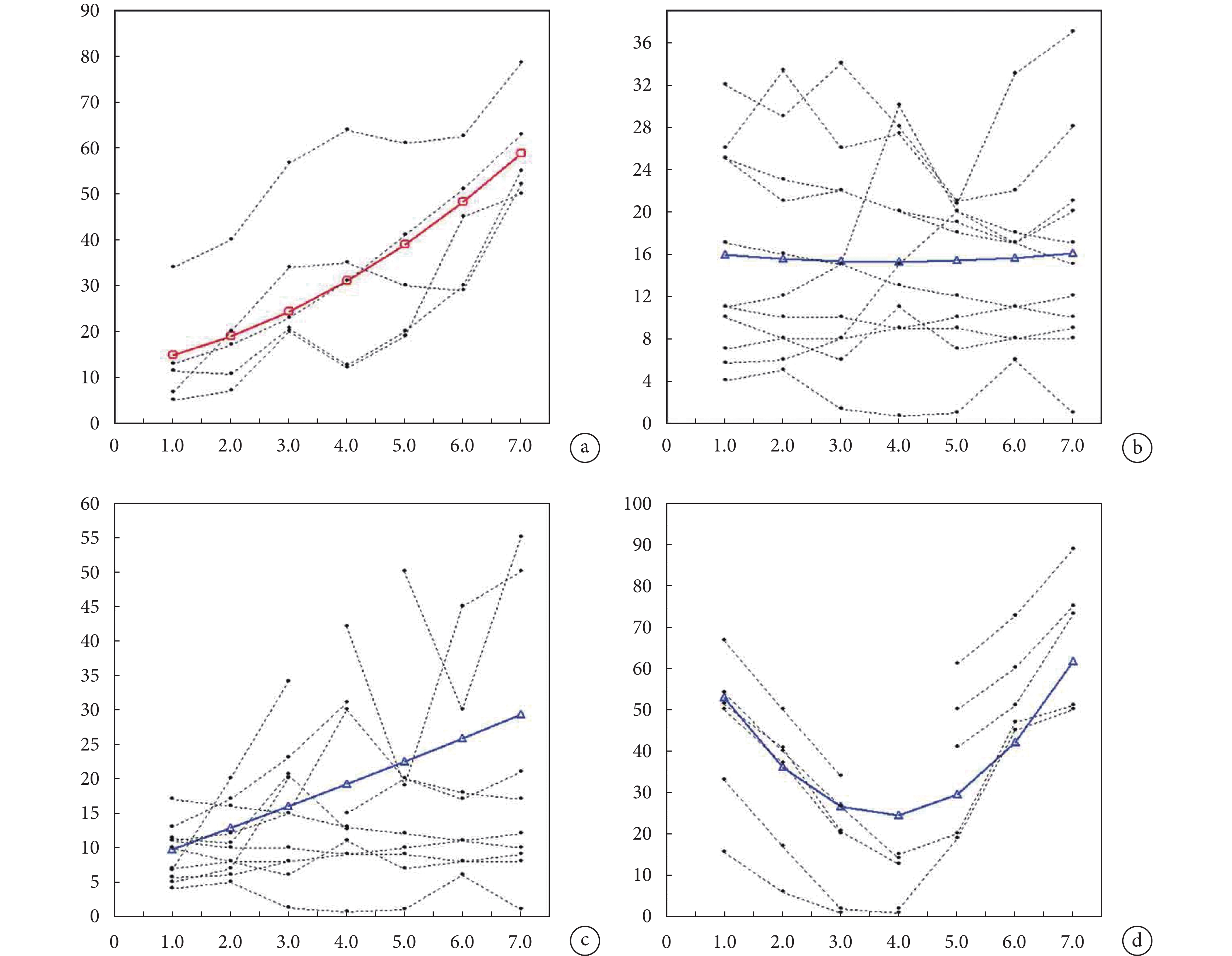 圖3
基于模擬數據的個體軌跡圖及估計均值
圖3
基于模擬數據的個體軌跡圖及估計均值
條目 15:是否用數字描述了最終潛類別模型的特征?
不僅需要呈現各模型下的潛變量軌跡圖,還需要呈現最終模型和每個模型各項參數的表格。具體包括:估計均值、標準差、P值、可信區間及用于估計每個模型參數的樣本量(注意任何缺失數據)。表格中的所有信息均應有助于讀者解讀結果,即使數據結果未在正文中完整報告,讀者仍應可獲得完整的模型結果。包含全部模型結果的表格還有助于實現結果報告的充分透明和完整重復。
條目 16:是否提供程序語句文件?
人們越來越意識到公開和透明的研究對維持和提高科學質量至關重要[86-90]。實現研究透明化的方式之一是共享數據、程序語句和其他支持材料(請參閱 Open Science Framework,https://osf.io/vw3t7/)。這些共享內容是所有論文的重要組成部分,它們讓其他研究人員可重現或改變論文中所報告的數據分析。此外,它們可使其他研究人員發現分析中的潛在錯誤,甚至是假的結果。公開程序語句文件是邁向完全公開數據和其他材料的第一步。多種方法可為讀者提供語句文件:如以附錄的形式呈現、通過在線補充材料或在線數據存儲庫來提供。語句信息最好不要僅在個人網站上展示(因為個人網站不是永久性的,可能會在某天關閉)。此外,一些新工具可助力語句的可及性。例如由 Center for Open Science 開發的在線協作工具,研究團隊可通過該工具將其研究材料的任一部分公開,以支持開放交流。Center for Open Science 還創造了一些“徽章”來證明論文滿足了開放材料要求。這些發展提示程序語句文件不應遠離讀者。我們的文件可在 Open Science Framework(https://osf.io/vw3t7/)上找到。
3 GRoLTS 在潛變量軌跡研究系統評價中的應用
為評估 GRoLTS 的一致性、有效性和可用性,我們利用 38 篇使用潛變量軌跡分析(即 LGMM 或 LCGA)來評估創傷事件后 PTSS 變化的研究對該報告規范進行了測試。每篇文章的平均評估所需時間為 20 分鐘,每篇論文評價由兩名評價員獨立進行。當得分相互矛盾時,評價員在快速陳述各自打分理由后,很容易便能達成共識。參考文獻的完整列表和相關細節請參閱 Open Science Framework(https://osf.io/vw3t7/)。
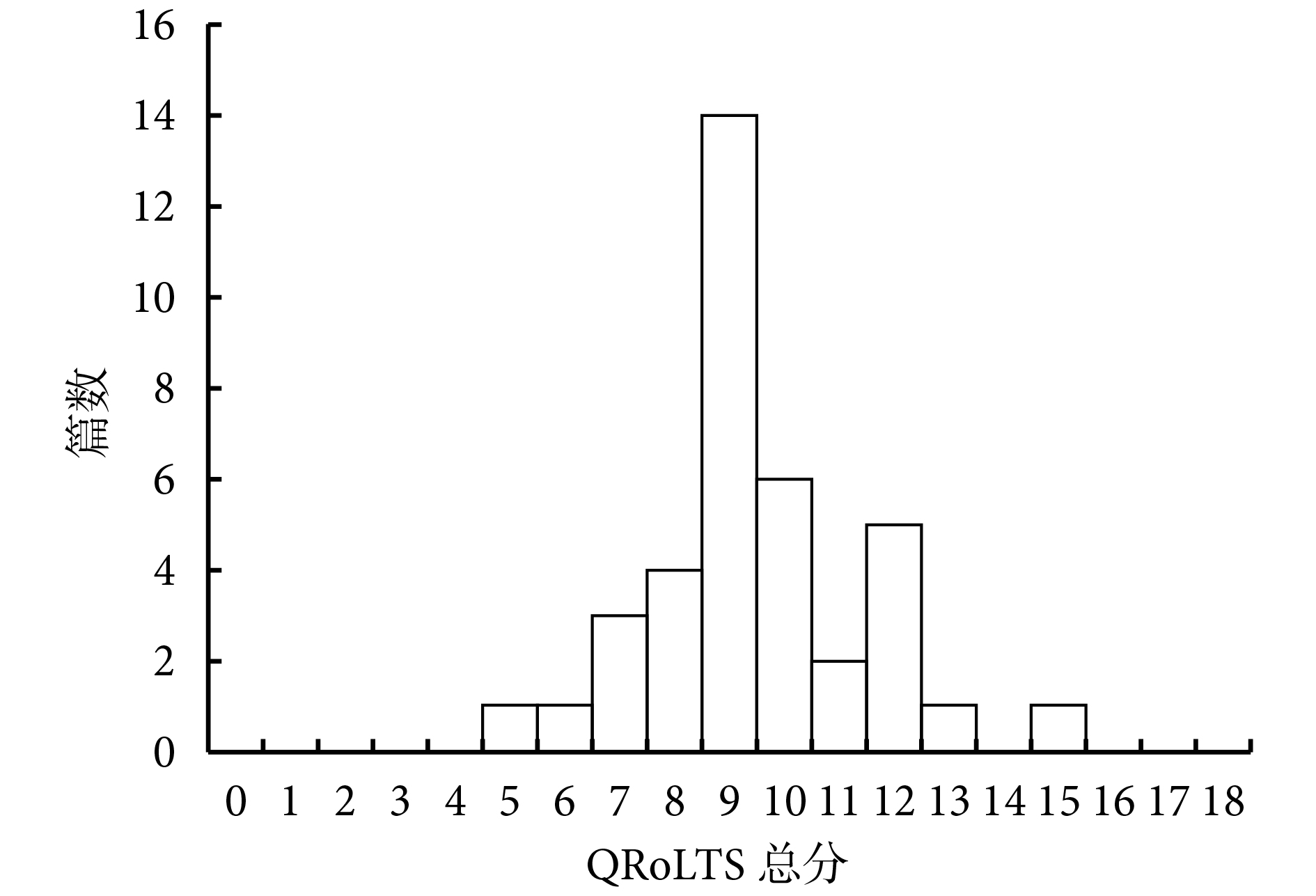
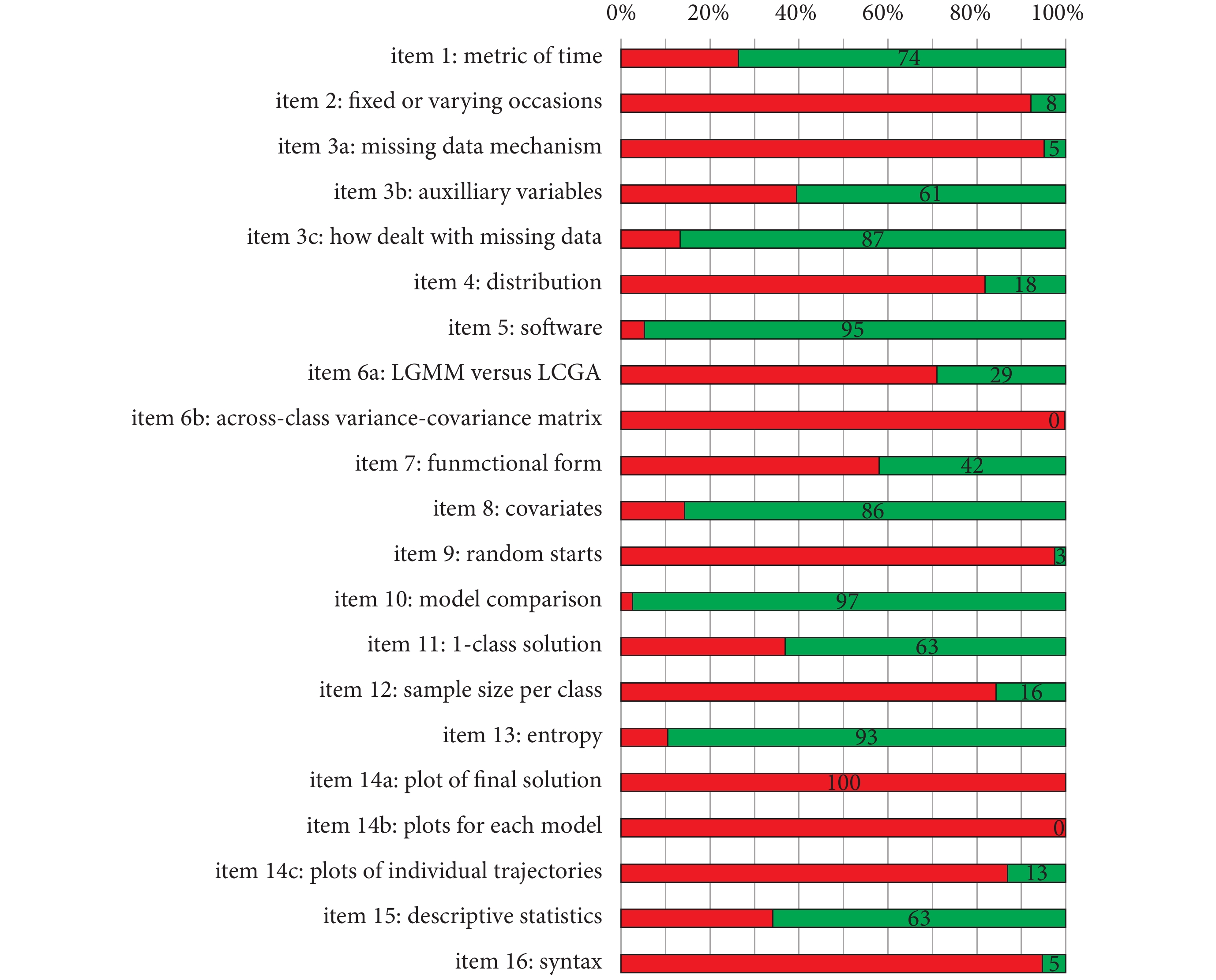
圖 4 展示了所有論文的 GRoLTS 總分,沒有一篇論文接近最高分 21 分(均值±標準差:9.47±1.97 分,范圍:5~15 分)。在檢查了具體的 GRoLTS 條目后(圖 5),我們發現一些條目在所有論文中幾乎都報告過,而有些條目幾乎從未報告過。我們將重點介紹最常報告和最少報告的前六個條目。
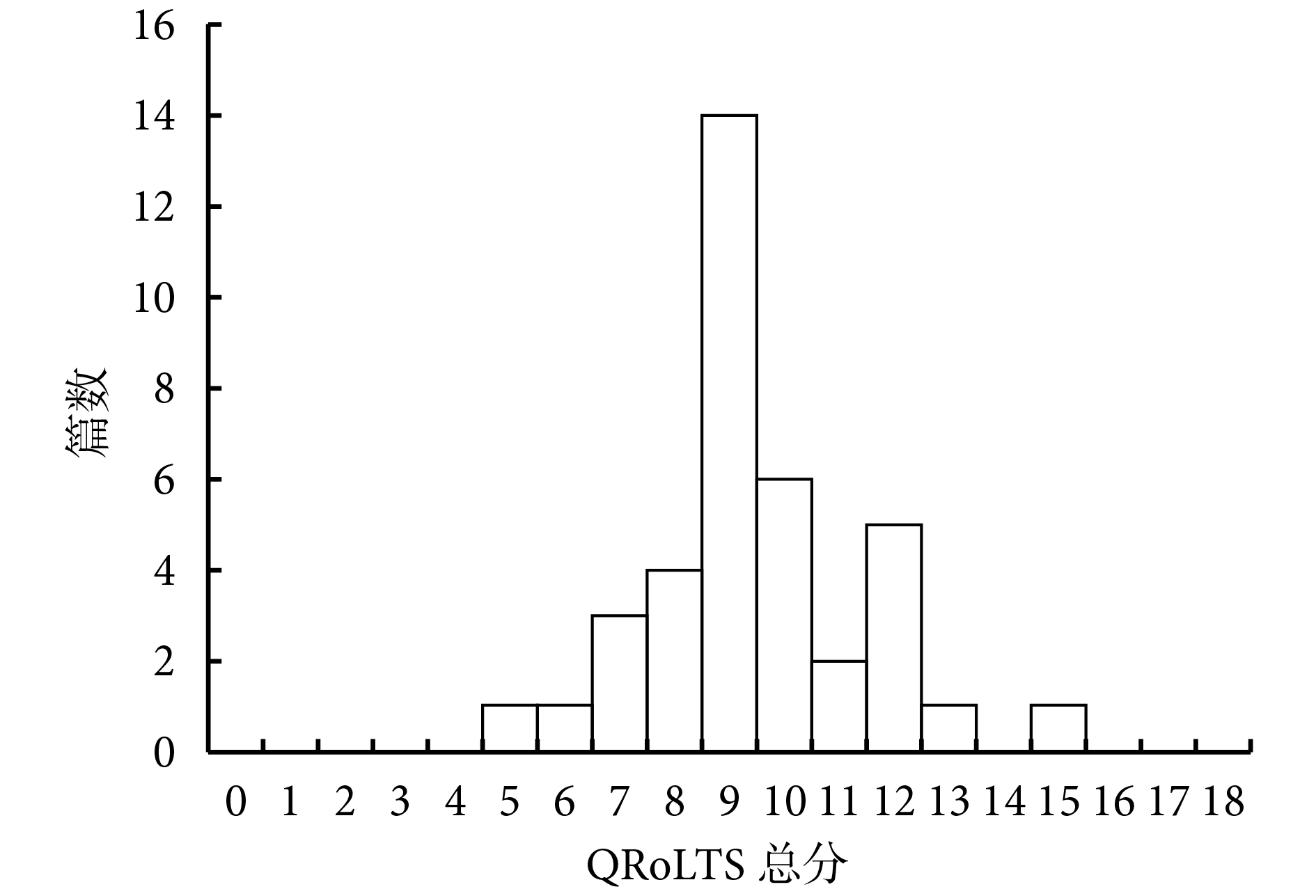 圖4
38 個采用潛變量軌跡分析探討創傷性應激癥狀發展的研究的 GRoLTS 總分
圖4
38 個采用潛變量軌跡分析探討創傷性應激癥狀發展的研究的 GRoLTS 總分
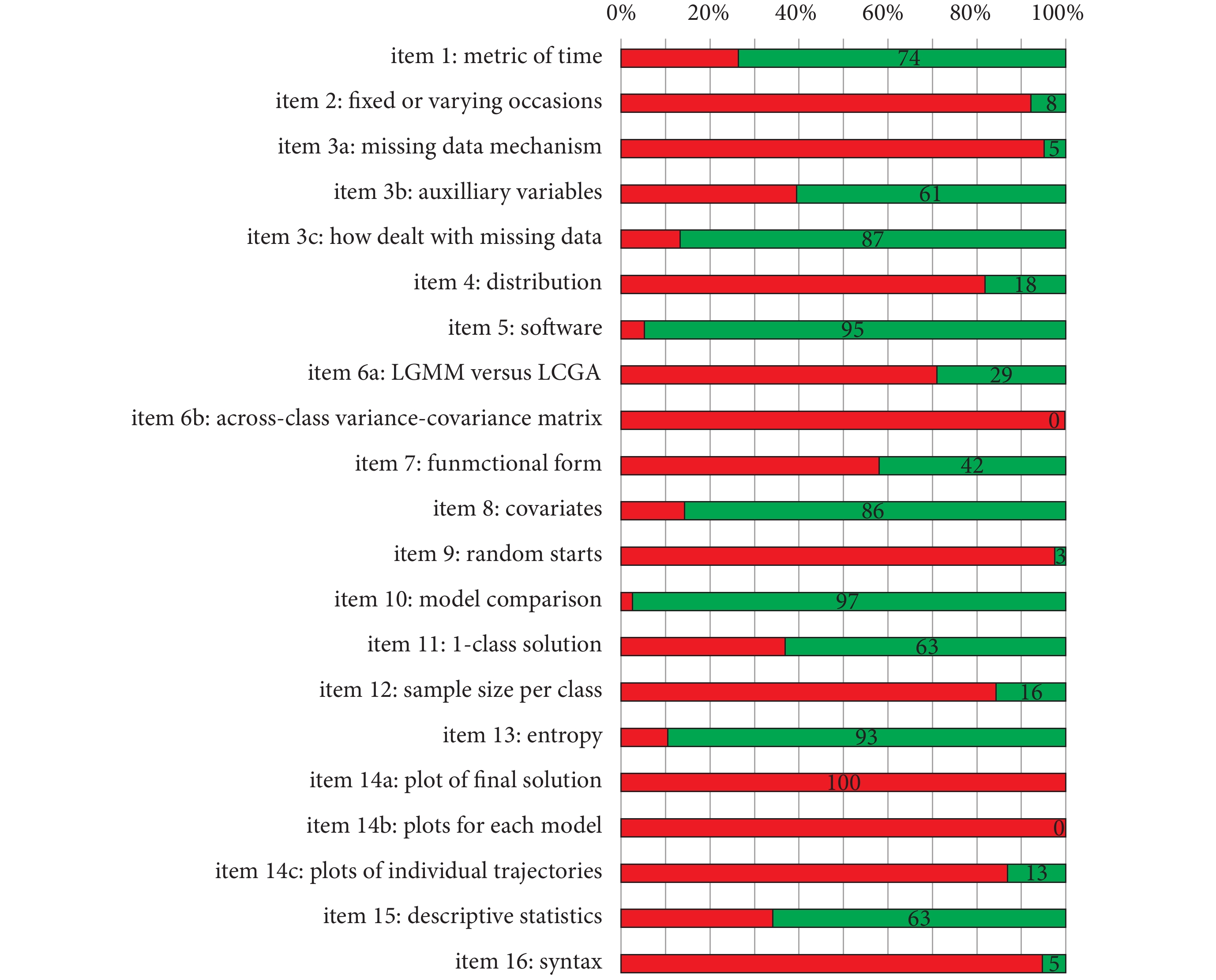 圖5
文章報告各項 GRoLTS 條目的比例
圖5
文章報告各項 GRoLTS 條目的比例
LGMM:潛變量增長混合模型;LCGA:潛類別增長分析;系統評價納入文章數量
3.1 最常報告的六大條目
3.1.1 條目 14a
所有文獻都提供了最終模型的估計平均軌跡圖(條目 14a)。
3.1.2 條目 10
幾乎所有文獻(97%)都報告了使用的模型選擇工具(條目 10),尤其是 BIC。約 2/3 文章還提到了其他模型選擇工具:SS-BIC 占 60.5%,AIC 占 63.2%,LRT 占 65.8%,BLRT 占 60.5%。12 篇文獻中提到模型擬合指數不一致,9 篇文獻中 AIC 或 BIC 不斷降低,10 篇文獻中基于統計標準的最優模型沒有意義,5 篇文獻中最佳模型中的一個類別僅覆蓋幾個人。一些文獻在模型選擇工具方面沒有提供簡單的潛類別估計結果,13 篇文獻僅根據理論而不是統計值來選擇模型。
3.1.3 條目 5
95% 的文獻報告了所用軟件(條目 5),其中 Mplus 最為常用(29 篇論文),其次是 SAS Proc Traj(7 篇文獻);30 篇文獻(79%)還報告了所用軟件版本。
3.1.4 條目 13
95% 的文獻報告了熵水平(條目 13),其熵值的中位數為 0.85。
3.1.5 條目 3c
89.5% 的文獻報告了如何處理缺失數據(條目 3c)。處理缺失數據最常用的方法為完整信息 ML(24 篇論文):但其中只有 1 項研究將這種方法與輔助變量相結合,3 項研究表明使用 MI 處理缺失數據。
3.1.6 條目 8
86% 的文獻對協變量(條目 8)進行了清晰描述。15 篇文獻使用了一步法,14 篇文獻使用了標準三步法(即分別保留最可能的類別成分與分析數據),只有 3 篇文獻使用了最近提出的 Vermunt 調整錯分三步法。
3.2 最少報告的六大條目
3.2.1 條目 14b/14c
沒有一篇 PTSS 文獻具體展示了每個模型的軌跡圖(條目 14b),僅有 5 篇文獻(13%)報告了最終估計平均軌跡與觀測到的個體軌跡(條目 14c)。但未報告此類軌跡圖(條目 14b 和 14c)并不局限于 PTSS 研究,在 Piquero[6]和 Erosheva[44]等人的系統評價中,分別發現 87 篇中有 0 篇、200 篇中僅有 8 篇(4%)軌跡研究報告了軌跡圖。
3.2.2 條目 6b
無一篇文獻報告了組間方差-協方差矩陣結構(條目 6b)。雖然從統計學角度來看組間方差-協方差矩陣結構十分重要,但顯然研究人員認為使用統計分析軟件默認的設置即可。
3.2.3 條目 9
僅有 1 個研究報告了所用的確切起始值數量(條目 9)。
3.2.4 條目 16
僅有 2 篇文獻中報告了公開程序語句文件(條目 16)。
3.2.5 條目 3a
僅有 2 篇文獻報告了缺失數據機制(條目 3a),且機制為 MAR。
3.2.6 條目 2
僅有 3 篇文獻報告了時間的變異性(條目 2)。
4 實例解讀
本節以美國西北大學的 Lloyd-Jones 等開展的一個隊列研究(coronary artery risk development in young adults study,CARDIA)[91]的縱向軌跡分析結果為例,利用 GRoLTS 清單進行評價,見表 3。
該文章于 2019 年 11 月發表在JAMA Cardiology,主要研究目的是探討從幼年到成年的 20 年間的蛋白尿軌跡與超聲心動圖測量的心肌結構和功能的關系,采用尿白蛋白與肌酐比值(urine albumin-to-creatinine ratio,UACR)測量蛋白尿的水平。
總體而言,針對 GRoLTS 清單的 21 個條目,該文章有 8 個條目未報告,有 2 個條目報告不充分,評分為 12 分。雖然原作者在文章的方法學部分較為詳細地描述了統計分析方法,但在結果部分的報告不太充分。
5 討論
本研究所制訂的 GRoLTS 是一種報告潛變量軌跡研究的工具(LGMM 或 LCGA)。研究者按照系統化的制訂流程,遵循專家小組和高級研究人員的意見,確定了報告軌跡研究結果必要的關鍵條目。無論文獻使用了何種統計模型,相應的報告規范都十分重要。其他報告規范,如隨機對照試驗報告的 CONSORT 清單,已被成功地推廣和應用。有系統評價表明,使用諸如 CONSORT 之類的報告規范確實提高了報告質量[92]。在潛變量增長軌跡模型研究領域,報告規范是呈現模型結果時必須要遵守的組成部分,其結果解釋在很大程度上與模型范式和估計的相關要素密切相關。
研究者建議所有潛變量增長軌跡模型都按照 GRoLTS 進行報告,以促進研究結果的合理呈現。需注意,GRoLTS 并非旨在衡量論文本身的質量,而是評估潛變量軌跡模型關鍵問題的報告質量。GRoLTS 條目全面而簡潔,雖然 GRoLTS 內容較為詳細,但很多條目僅需通過在論文中增添一些句子或使用在線補充材料即可滿足。GRoLTS 可供準備提交稿件的作者使用,也可作為期刊審稿時對 LGMM 或 LCGA 研究的報告規范。由于 LGMM 或 LCGA 研究發展迅速且在不同領域中廣泛應用,因此 GRoLTS 應該定期更新和修訂,必要時應進行條目添加或刪除。據研究者了解,軌跡方法在不同領域、不同類型的研究問題間存在較大差異。因此,報告軌跡結果時,還需考慮是否有 GRoLTS 未涵蓋的其他要點。
研究者想以 Bauer[93](第 782 頁)的一句話結束本文:“我試圖解決的基本問題是這些模型(指 LGMM/LCGA 模型)是否有可能推動心理學的發展。我確信,如果這些模型繼續按照目前的方式使用,那么答案顯然是否定的……因此,我認為,除非分析背后的理論和數據都非常成熟,否則應避免直接使用 GMMs。否則,GMMs 在心理學研究中的應用可能偏離正確發展方向而走入死胡同。”
研究者同意 Bauer 的觀點,因過去這些模型的報告方式既不透明也不一致,難以產生可靠的、可重復的結果。如果所有相關領域的研究人員都具有扎實的理論基礎并形成使用 GRoLTS 規范報告的習慣,那么相信采用潛變量增長軌跡建模將會得到進一步發展,并成為應用統計學中最透明和最可重現的領域之一。
資助 van de Schoot R 和 Vermunt JK 分別得到了荷蘭科學研究組織的資助:NWO-VIDI-452-14-006 和 NWO-VICI-453-10-002。
致謝 感謝在德爾菲研究不同階段提供反饋意見的專家(按字母順序):Heather Armstrong、Daniel Bauer、George Bonanno、Jan Boom、Patrick Curran、Isaac Galatzer-Levy、Christian Geiser、Kevin Grimm、Joop Hox、John Hipp、Loes Keijsers、Lynda 和 Dan King、Todd Little、Gitta Lubke、Peter Lugtig、Katherine Masyn、BengtMuthén、Daniel Nagin、Karen Nylund、Cecile Proust-Lima、Quinten Raaijmakers、Jost Reinecke、Paula Schnurr、Geert Smid。
注釋
① 通過潛變量軌跡分析,我們采用基于個體的分析技術來估計隨時間推移發展的未觀測到的個體亞組潛分類[1]。為了估計軌跡潛分類,將傳統潛變量增長模型[2]與混合成分[3]相結合。潛變量增長模型的基本思想是假設所有個體都來自同一個人群。當結合混合模型時,假設增長參數(截距、斜率等)在預先指定和未觀測到的亞人群間是變化的。這可通過使用分類潛變量來實現,分類潛變量允許各組有單獨的增長軌跡,并為每個(未觀測到的)組產生單獨的潛變量增長模型,每個模型都有其獨特的一組增長參數。
② 當小規模的潛類別是研究目標時最好選擇貝葉斯估計,其在小樣本 LGMM 和 LCGA 模型中的表現優于 ML 估計[78]。
③ 類別區分度指的是不同潛類別在統計上或實質上的差異。類別區分度可基于多種不同的軌跡特征,包括具有明顯區別的截距或斜率、不同的軌跡形狀(線性增長 vs. 非線性增長)、不同的潛變量增長因子協方差結構等[78]。
參考文獻
見原文。
估計潛變量軌跡的研究方法在社會學、行為學和生物醫學領域越來越流行[1-3]。因其在混合模型框架下進行模型估計的過程中會涉及多個決策過程,選擇不同的決策方案會在一定程度上影響研究結果,甚至可能產生不同結論。盡管目前潛變量軌跡分析十分受歡迎,并成為了許多領域內分析縱向數據的主流工具,但尚無潛變量軌跡模型結果的報告標準。這導致了論文中對潛變量軌跡分析結果的報告存在很大差異,而不充分或不完整報告潛變量軌跡分析結果會妨礙對結果的解讀和批判性評價,并且影響不同研究間結果的橫向比較。
本文介紹潛變量軌跡研究報告規范(guidelines for reporting on latent trajectory studies,GRoLTS)。GRoLTS 的最終目標是提高潛變量軌跡研究報告的一致性,使研究結果可完全透明(高質量)地呈現,并且可用于研究間的比較、重復、系統評價和 Meta 分析等。在本文中,我們將首先描述 GRoLTS 的制訂過程,即采用系統化的制訂過程,通過 4 輪德爾菲法,由專家小組確定報告軌跡研究結果必要的關鍵條目;隨后詳細描述每一個關鍵條目內容;最后,介紹利用 GRoLTS 評估 38 篇使用潛變量軌跡分析探討創傷后應激癥狀(posttraumatic stress symptoms,PTSS)變化研究的報告情況。更多相關信息請參閱 Open Science Framework(https://osf.io/vw3t7/),包括:① 德爾菲研究的全部細節;② 可用于教學的部分條目的補充信息;③ 篩選 38 篇 PTSS 論文的數據集。
1 GRoLTS 的制訂
GRoLTS 的制訂過程包括以下階段[4]:① 初步確定主題;② 形成條目;③ 評估表面效度;④ 評估一致性和結構效度的現場試驗(field trials);⑤ 制訂最終的精煉條目清單。
指南制訂之初,制訂小組明確了 GRoLTS 需符合以下基本要求:① 適用對象為探索性使用潛變量軌跡分析來回答實質研究問題的論文;② 總結報告潛變量軌跡分析結果的要求;③ 確保不同背景的研究人員能夠一致、可靠地使用此報告規范進行報告;④ 條目簡明扼要易于完成,同時應包括確保結果可重復性和透明性的所有方面。
在制訂階段,制訂小組共邀請 27 名專家(參見致謝中的專家名單),并向他們提供了 GRoLTS 的制訂目標和要求,通過前 3 輪德爾菲法和第 4 輪現場試驗評估所有條目的表面效度。制訂小組采用德爾菲法在專家小組中就 GRoLTS 應包括哪些標準及具體條目的措辭達成一致。以上每個步驟的具體細節,包括 GRoLTS 的所有前期版本請參閱 Open Science Framework(https://osf.io/vw3t7/)。
2 GRoLTS 條目和解讀
GRoLTS 包含 16 個條目(部分含子條目,表 1)。每個條目評分為 0(未報告)或 1(已報告)。建議在如下情況使用 GRoLTS:① 研究人員準備提交論文前;② 編輯、審稿人和授權專家核查論文是否報告了所有基本要素;③ 老師向學生講解潛變量軌跡分析結果中哪些要素是重要的。我們將對每一個條目(特別是復雜的條目)進行解讀,并對文獻中討論內容進行概述。關于條目 1、2、7 和 14 的更詳細信息請參閱 Open Science Framework(https://osf.io/vw3t7/)。
條目 1:是否報告統計模型中所使用的時間度量?
在任何類型的增長模型中,時間編碼對結果解讀都具有重要意義。如 Eggleston 等[5]研究所示,隨訪時間長度會影響潛變量軌跡的數量,形狀-時間越長,軌跡越多。此外,Piquero[6]對基于犯罪數據的潛變量增長混合模型(latent growth mixture modeling,LGMM)和潛類別增長分析(latent class growth analysis,LCGA)進行系統評價后發現,時間點的間隔也會影響軌跡數量。因此,不僅要透明地報告時間度量,更要正確地設定時間點間隔。時間度量的設定應該在分析開始前依據研究設計確定,而非根據模型的擬合程度或增長參數的顯著性。關于時間度量更深入的討論請參閱 Open Science Framework(https://osf.io/vw3t7/),及 Biesanz 等[7]或 Duncan 等[8]的研究。
條目 2:是否提供單個隨訪的均數和標準差?
在縱向研究中,由于組織安排的原因,對不同研究對象進行多次數據采集時,不同個體間的采集時間間隔必然存在一些差異。這種差異被稱為時間-非結構化數據或隨訪內變異。與之相對應的是時間-結構化研究,即所有研究對象的數據均以相同的時間間隔采集。在某種程度上,絕大多數縱向數據是時間-非結構化的。也就是說,并非所有研究對象都在相同的時間點采集數據,請參閱 Palardy 等[9]的實例。然而,時間-非結構化數據往往會被研究者忽略時間的非結構化特性,而按照時間-結構化數據進行分析,這可能嚴重曲解分析結果真實性。Singer 等[10]發現,當使用預期年齡而非實際年齡作為時間度量時,會高估線性斜率、截距和線性斜率的方差。Mehta 等[11]、Hertzog 等[12]及其他幾個模擬研究[13,14]也得出相似的結論。我們建議,在每個數據集中納入一個時間變量,用于記錄不同觀測點間的確切時間間隔,以便能夠在方法部分計算并報告時間間隔的變異程度。因此,可使用隨個體觀測時間變化的隨機因子載荷替代固定因子載荷(更多細節請參閱 Coulombe 等[14])。更詳細的解釋和圖解說明請參閱 Open Science Framework(https://osf.io/vw3t7/)。
條目 3a:是否報告缺失數據機制?
大多數縱向研究存在缺失數據或研究對象失訪問題。在描述缺失數據和失訪情況時,應首先報告數據缺失機制。數據缺失機制一般可分為三種類型[15]:① 完全隨機缺失(missing completely at random,MCAR),即所有缺失數據的發生不依賴于所有觀測到或未觀測到的變量;② 隨機缺失(missing at random,MAR),即缺失數據可能依賴于觀測到的變量,但不依賴于未觀測到的變量;③ 非隨機缺失(missing not at random,MNAR),即缺失數據依賴于未觀測到的變量。我們無法判斷數據缺失屬于 MAR 還是 MNAR(因無法檢驗),只能盡量保證數據的缺失符合 MAR 假設。統計模型如 LGMM/LCGA 的假設均基于 MAR。因為對所有研究對象均進行了多次測量,只要失訪不是以某種特定方式系統性地發生,在縱向隊列中就可假定該失訪滿足 MAR 情況(即這些個體的觀測變量得分的缺失,可假定是隨機的)。
條目 3b:是否描述與失訪或缺失數據相關的變量?
正如 Asendorpf 等[16]的研究所示,對于縱向研究,即使每一輪隨訪中微小且不顯著的選擇性退出,效應也會在整個隨訪過程中逐漸累積,最終導致結果產生越來越大的偏倚[17]。因此,研究者應比較退出與完成研究的對象的相關特征。與失訪或缺失相關的變量(也稱輔助變量)可作為模型中的協變量(服從 MAR 假設下擬合)或可在多重填補(multiple imputation,MI)模型中使用。使用 MI 的優點是可將缺失數據的處理與目標模型區分開來。
條目 3c:是否描述分析過程中缺失數據的處理?
關于缺失數據報告的第三個問題是在分析過程中如何處理缺失數據。在許多論文中都引用了 Peeters 等[18]對不同填補模型的比較。目前,處理缺失數據較為普遍和靈活的方法是利用鏈式方程的多重填補(也稱預測均值匹配)[19,20]。
條目 4:是否納入觀測變量分布類型的信息?
潛變量軌跡分析中的因變量可存在不同形式。通常假設變量是連續型且在組內呈正態分布,但實際上并非總是如此。因變量可能不是連續型變量,而是分類變量(如,具有五個應答類別的李克特式量表)、計數資料(如,計數某人的癥狀數量)或零膨脹型(如,80%~90%的研究對象得分為 0)。正如 Vermunt[21]所述,假設組內因變量呈正態分布至關重要,當假設因變量在組內呈多項分布(非正態分布)時,建議不使用連續型變量混合模型,應轉而使用離散型變量混合模型。Bauer 等[22-24]研究發現,當變量分布的假設不成立時(即當實際的結局分布為非正態分布時),即使結果只呈現一組軌跡[25]也更傾向于選用多軌跡群組模型,只要在統計分析軟件中設定研究結局的類型,潛變量軌跡框架就可輕松處理該類變量,并避免過度提取潛類別。另一種方法是使用潛變量[26],即通過使用單個條目分數而非總分來考量結局的測量結構。如果模型中的潛變量有意義,那么潛變量和調查條目的測量結構應該隨時間穩定,即測量結構不隨時間變化而變化。以上是一個需要檢驗的重要假設,又被稱為測量不變性[27],雖然該假設并不總是成立,但該假設會對結果產生較大影響[28]。
條目 5:是否提及統計分析軟件?
目前可用于估計潛變量軌跡的程序包有以下幾種:LatentGold[29]、Mplus[30]、SAS Proc Traj[31]、Stata GLLAMM[32]、R 程序包 LCMM[33]、R 程序包 OpenMx[34]等。這些程序包指定默認模型的方法均有所不同。例如,Mplus 的默認設置是在組間限制協方差和(殘差)方差。相反,在 LatentGold 中則使用先驗殘差進行后驗方法估計,以防止殘差變為 0。出于可重復性的考慮,提供使用的軟件及版本信息至關重要(因為版本更新可能涉及到后臺算法調整)。在下一個條目中,我們會進一步討論方差-協方差矩陣的設定。
條目 6a:是否考慮并清晰記錄處理組內異質性的方式(如 LCGA 或 LGMM)?
在建立潛變量軌跡模型時,為精確地指定模型需要做許多選擇。處理組內異質性的第一種方法,涉及潛類別內增長參數的方差。有兩種潛變量增長模型可解釋未觀測到的群體。如果在潛變量軌跡內估計增長參數的方差,則這種建模靈活性稱為 LGMM[1,35-38]。如果假設組內所有個體增長軌跡是同質的,且假設組內增長因子的方差和協方差估計值固定為 0,則稱為 LCGA[39-42]。Groudace[43]、Erosheva[44]、Feldman[45]、Jung[46],Kreuter[47]和 Twisk 等[48]很好地總結了 LGMM 和 LCGA 間的區別。
Nagin[39,41]運用理論方法并引入潛變量軌跡模型的兩個概念:① 作為群體異質性連續但未知分布的近似值;② 作為具體的軌跡,可視為非常重要的實體。在第二種概念中,該軌跡有描述性名稱,并作為不同的實體進行討論。Erosheva 等[49]的系統評價表明,大多數研究人員采用第二種方法(第 325~326 頁),但能夠真正發現不同軌跡組別的情況其實十分罕見。正如參與本指南解讀的一位專家所說:“我還沒遇到過一種能夠明確表述的發展理論,它能先驗地參數化增長因子組內方差-協方差的結構。”Twisk 等[48]認為應從可行性角度出發選擇研究方法。由于 LGMM 算法較難,研究人員常選用 LCGA。但實際上 LGMM 更靈活,因為該方法考慮了前面提到的組內變異帶來的異質性問題,但這種靈活性也帶來了一定的問題:如需要更強的計算能力、需要更大樣本量、可能引發收斂問題等。既往在專業期刊如Infant Child Development上,已對使用何種參數化方法這一問題進行了激烈討論[25,37,50,51]。本文對這一問題不再贅述,只強調應在論文中討論最終模型的選擇。理想情況下,應采用兩種模型擬合數據并進行比較。提出此建議的原因是實際結果會因模型選擇的不同而異,因此檢查每種方法對于理解其對最終模型解釋的影響非常重要。
條目 6b:是否考慮并清晰記錄處理組間方差-協方差矩陣結構差異的方式?
除 LGCA 和 LGMM 間的差異外,第二個問題是約束誤差結構(相較于不同類別中自由估計)。約束誤差結構與不同類別間增長因子方差-協方差矩陣的異質性(相較于同質性)相互影響。也就是說,潛類別間的殘差和方差-協方差矩陣是相同的,還是不同的?以下原因可解釋為什么殘差在潛類別間保持不變或各潛類別具有特定的殘差:潛類別間殘差相同是以偏離增長曲線的變異在組間沒有差異為假設,而潛類別間殘差不同則是以某些組(這里指潛類別)偏離增長曲線的變異要大于其他組為假設。組內特定的殘差可能更符合實際情況,然而由于模型包含多項參數,因此該情況可能引發估計問題。此外,若使用連續數據模型分析離散數據,則會出現殘差為零的情況。我們建議研究人員應基于已知、具體的信息及分析過程中出現的估算問題選擇相應模型。
是否約束潛類別間方差-協方差矩陣更需要考慮現實問題。雖然每個潛類別都允許存在特定的方差-協方差矩陣,但由于模型需要估計大量參數,因此需要更大的樣本量來避免收斂問題。對于較小樣本量的解決方法是分別估計方差-協方差矩陣,研究人員多采用約束方差-協方差矩陣來簡化模型(或處理局部極大值的誤差信息)。無論采用何種方法設定組間方差-協方差矩陣,研究人員都應在論文中明確報告,因為不同設定均會對研究結論產生實質性影響。具體來說,研究人員應盡可能清楚地列出所有使用的研究方法及原因(如,“理論表明增長因子的變異在亞組間是恒定的,因此我們認為矩陣相同”等)。其次,研究人員應根據所作假設解釋結果。需注意的是,若重新定義方差-協方差矩陣,結果也可能隨之改變。例如,如果協方差矩陣改變(如各類別間自由估計),則潛類別的估計結果也會隨之改變并產生完全不同的解釋。
條目 7:是否描述軌跡的形狀和函數形式的設定?
令趨勢線變化的主要方法之一是指定用于捕獲隨時間變化的增長函數。基于多項式函數的增長模型通常用于估計線性、二次、三次等變化[38]。然而,增長不需要通過多項式函數估計。許多非線性參數模型也常用于估計增長,例如 logistic、Gompertz 和 Richards 增長曲線[52]。平滑函數的半參數模型,如廣義加性模型,同樣可用于估計增長[53];此外,還可使用分段模型[9,54]。我們建議不僅要報告每條軌跡在最終模型中的形狀,還需要根據指定函數驗證模型:例如,比較線性增長模型與包含二次效應模型的結果。關于不同形式的增長函數是如何影響增長參數解釋的問題,請參閱 Open Science Framework(https://osf.io/vw3t7/)。
條目 8:如果納入協變量,分析是否仍可重復?
預測因素(或協變量)可在 3 個不同水平添加到模型中(圖 1):① 在因變量水平上作為依時或非依時協變量納入,以控制在特定時間點的變異;② 在增長參數水平上納入,以尋找不能通過協變量個體差異(如年齡、膳食、社會經濟狀況)解釋的潛類別;③ 在自變量水平納入,以預測潛分組。如果協變量被指定為模型的一部分,那么該模型通常被稱為條件模型;而非條件模型是指在忽略協變量的情況下探索潛類別數量。需注意的是,無論預測因素出現在模型中的哪個位置,它們既可是直接觀測到的變量也可是潛變量。目前有多種方法可用于預測潛分組,我們將在下文逐一介紹。
 圖1
潛變量軌跡分析模型示例
圖1
潛變量軌跡分析模型示例
該模型包括 1~8 個類別(C=1,…,8),8 個重復測量變量(創傷后應激障礙,posttraumatic stress disorder,PTSD 等),3 個增長參數(截距、斜率、二次項)和可添加協變量的 3 個位置。
一步法:在聯合模型中可納入潛分組的預測因素,該模型可同時估計組別和預測潛分組。一步法有兩個缺點:第一,納入的預測因素可能會不適當地修改潛類別結構的構成。理論上,模型中的任何改動都會影響潛類別下個體的劃分。由于協變量會影響潛類別的形成,所以在模型中直接加入預測因素會導致結果的缺陷。此外,因為潛變量是通過測量指示變量獲得,直接加入預測因素可能使潛類別失去意義(第 329 頁)[55]。La Greca 等[56]詳細描述了這種效應(第 360 頁)。在這種特定情況下,應重新考慮潛類別數量,而不是繼續采用在沒有納入協變量的情況下所確定的類別數量。無論改變潛類別估計結果的效應是否對研究人員有意義,對于在模型中納入或不納入協變量的標準仍不明確;參閱 Palardy 等[9]的研究,其根據所需的潛類別數量比較了有、無協變量模型的區別。總之,希望研究人員不要將選擇主要預測因素的問題與發現潛類別數量的問題混為一談。第二,受影響的還有一個稱為熵的指數(另見條目 13)。熵的作用是評價將個體劃入各潛類別這一分類過程的準確性,反映了根據個體軌跡和協變量值預測潛分組的水平。若熵值接近 1.0,則認為進行了適當的分類;若熵值接近 0,則認為分類效果較差。采用人工納入預測因素的一步法會人為地高估熵指數,導致過于夸大分類的可信度。而且,熵本身的含義也在變化。
標準三步法:保留最合適的潛分組并分別分析數據 按照該策略,首先在沒有潛分組預測因素的情況下確定潛類別的數量(步驟 1)。隨后保留最合適的潛分組與原始數據合并(步驟 2),并采用多項式回歸分析將其與潛變量軌跡模型分開分析(步驟 3)。Andersen 等[57](補充材料,第 2 頁)和 Pietrzak 等[20](第 208 頁)清晰描述了該方法。盡管該方法采用了最合適的潛分組策略來解決了一步法存在的各種問題,但它忽略了潛類別分配的不確定性。換句話說,該策略假設個體在潛類別分配中不存在錯分。其結果是,基于協變量的預測可能低估真實效應。但是可通過熵來評估低估程度:熵值越高,錯分越少,潛分組預測結果偏倚越小[58]。保留最合適的潛分組策略要求熵值足夠高,且作者承認衰減效應。
使用“偽分類”方法的三步法:由 Wang 等[59]提出的方法是:首先估計潛類別模型,然后基于從模型中獲得的后驗分布采用 MI 處理潛類別變量,隨后使用由 Rubin 等[60,61]提出的 MI 技術,分析填補的潛類別變量和協變量。Peutere 等[62](第 17 頁)詳細地描述了該策略。與前文提及的其他方法相同,若使用偽分類方法,研究人員應進行明確地描述,并且說明潛類別變量是通過 MI 獲得。
調整錯分三步法:該方法由 Vermunt[3,63]在 Bolck 等[64,65]的思想上發展而來。與前文中的三步法不同,該方法考慮了第三步分析中潛類別分配下的錯分問題,即估計所得潛分組并非真實的潛分組這一問題。實際上,估計潛類別模型,只是將步驟 2 中指定的潛分組作為單一指示變量,根據步驟 1 和 2 的估計值確定錯分概率(第 330 頁)[55]。該方法允許協變量在標準潛類別模型中預測潛分組,但也可通過潛分組預測遠端結局[66]。
調整錯分三步法與前文中提及的三步法具有相同的優點,即可將構建對目標響應變量有意義的潛變量軌跡模型與構建探究潛類別與外部變量關系的模型區分開來。但需注意,該方法同樣存在前提假設,除了要求外部變量和潛類別指示變量相互獨立之外,當外部變量為遠端結局時,還需正確設定遠端結局的組間分布。請注意,盡管可放寬條件獨立假設,但該假設同樣適用于一步法。針對遠端結局組間分布,Bakk 等[66]表示,即使偏離分布假設,BCH 變異[64]仍然穩定,但最大似然(maximum likelihood,ML)變異卻并不穩定。
總之,可在 LGMM 中的 3 個不同水平納入協變量(圖 1),并且當分析目標是預測潛分組時,至少有 4 種納入協變量的方法,同時也是納入協變量的常見原因。由于納入協變量的方式和方法對模型結果解釋有很大影響,在沒有明確推薦方法的情況下,作者對上述過程進行完全透明的報告極為重要。
條目 9:是否報告隨機起始值數量和最終迭代次數?
若使用 ML 估計潛變量軌跡模型,了解最終的潛類別估計結果是否已收斂到 ML 分布的最大值而不是所謂的局部最大值十分重要。因為 ML 函數有時不僅只有一個最大值,還可能存在幾個最大值,這種情況需要根據模型參數的起始值找到“真實”(即絕對)的最大值。因基于局部最大值(相較于真實最大值)的估計結果可能與最優結果有很大不同,所以強烈建議基于多個不同起始值重新運行模型,以確保找到最優解。在統計學文獻中已經非常詳細地討論了在估計混合模型時使用多組起始值的重要性。例如,Hipp 等[67]詳細討論了不恰當或起始值過少對結果的影響。研究發現,當起始值錯誤時估計結果可能有實質性的錯誤。每個估計的參數都有相對應的較為適當的參數空間,他們建議根據這些空間“明智地”確定每個參數的起始值。參數的起始值可隨機生成,但是在混合建模環境中,通常基于某些理論選擇這些參數。Finch 等[68]討論了基于某理論在潛類別分析中選擇閾值起始值以避免在錯誤的參數空間中探索估計算法的問題。此外,為充分探索參數空間并避免僅收斂到局部最大值,建議將每個參數的起始值數量增加到至少 50 到 100 組[67]。當研究人員基于某理論或既往研究設定起始值時,這些起始值集合包含了既往相關起始值的隨機波動,可確保所有集合覆蓋了可能的參數空間。
條目 10:是否從統計的角度描述模型比較(和選擇)工具?
多項統計標準可用于判斷模型對數據的擬合程度,即應當劃分出多少潛類別。Nylund 等[69]的大樣本模擬研究顯示,貝葉斯信息準則(Bayesian information criterion,BIC;Schwarz[70])的表現優于其他模型選擇工具如 LGMMs 背景下的 Akaike 信息準則(Akaike information criterion,AIC)[71]。兩者都是基于對數似然把參數數量作為模型復雜性的懲罰項,以此來評估相對模型充分性的模型選擇工具。從軌跡數量的角度來看,具有最小 BIC 值的模型最優(參見圖 2 中模型 2 的結果)。BIC 目前已有許多衍生形式,其中樣本量調整的 BIC 有時也用于潛變量軌跡研究。
 圖2
比較三個假設模型的貝葉斯信息準則值(BIC-1,BIC-2,BIC-3)
圖2
比較三個假設模型的貝葉斯信息準則值(BIC-1,BIC-2,BIC-3)
需注意,帶有一個星號的模型表示隨機啟動次數增加到 1 000,帶有兩個星號的模型沒有達到收斂。
由 Lo 等[72]提出的 Lo-Mendel-Rubin 似然比檢驗(Lo-Mendel-Rubin-likelihood ratio test,LMR-LRT)是另一種常用的模型選擇工具。LMR-LRT 檢驗k?1 個類別是否優于k個類別,若檢驗結果顯著,則表明拒絕k?1 個類別的零假設,接受至少k個類別。但 Jeffries[73](第 901 頁)指出,“該方法還未得到證實,模擬研究表明其結果可能不正確。”隨后,Nylund 等[69](第 538 頁)回應,最初在 Lo 等[72]的早期模擬研究表明,盡管如 Jeffries 所述,可能存在分析不一致性,但 LMR-LRT 仍可作為一種用于類別算法的有效檢驗工具。鑒于既往文獻中潛在的不一致,我們建議研究人員不要僅根據 LMR-LRT 工具確定類別數量。最近,有模擬研究證明 bootstrap 似然比檢驗(bootstrap likelihood ratio test,BLRT)[74]是選擇最優類別數量的良好指標[69],當將其應用于經驗數據時總會得到顯著結果。
盡管就評估擬合程度的方法仍有諸多爭議,但專家小組已經達成共識,推薦使用 BIC。當模型選擇工具和熵指數所確定的最優維度很大、各工具評估結果相互沖突或與理論沖突時,研究人員在實際操作中常將潛變量軌跡的數量減少至理論上有意義的數量。例如,研究人員通常會刪除只有微小變異的軌跡(如,Galatzer-Levy 等[75])或拒絕有收斂問題的模型(如,Orcutt 等[76])。
總之,我們建議研究人員如實描述選擇最終模型的過程。基于現有文獻,我們建議選擇 BIC 作為模型比較工具,但也建議研究人員使用多個工具來避免“選擇性失明”(即只看到有利于結論的證據,忽略不利證據)。請參閱表 2 和圖 2,了解如何選擇并使用模型比較工具(請注意,表 2 采用模擬數據用以舉例說明)。如類似表 2 情況,擬合指數在最優類別數量上不一致,應告知這一結果。作者應報告所有檢驗的模型,并最好結合理論對最終所選模型舉例說明(另見條目 14)。值得注意的是,有研究提出了許多可供選擇的指標[59]且該領域正迅速發展[77],因此研究人員應該及時關注該領域的新進展。
條目 11:是否報告擬合模型總數,是否包括僅含一個類別的模型?
軌跡分析的目的是找到描述數據集變異的潛類別的最優數量。為了找到類別最優數量,我們建議采用先從僅含一個類別開始的前進建模法,這是擬合效果最好的非混合潛變量增長模型。該模型簡單地假設群體中不存在亞組,隨著時間的推移所有個體或多或少遵循相同的軌跡。研究人員通常不會報告僅含一個類別的結果,但往往非混合模型能更好地擬合數據。圖 2 中模型 1 所示,假如不報告僅含一個類別的結果,根據 BIC 的值會選擇含三個類別的模型。但當報告僅含一個類別的結果時,BIC 提示一類別為最優模型。在這種情況下,結論則應為群體中不存在潛類別(即一類別為最優)。在擬合一類別模型后,應該逐步增加類別以確定哪個模型擬合最好。當模型擬合指數不再優化時也不應停止此過程,應該繼續擬合至少一或兩個額外的模型,以確保所有可能的模型都納入了分析。
條目 12:是否報告每個模型下每組所含個體數量?
確定最終類別數量時不應僅基于統計標準。例如,統計上的最優解軌跡可能只含有非常少的研究對象。當兩個群組(即潛類別)的規模明顯不同時(如一個群組遠大于另一個),大的群組會覆蓋小的群組,從而導致對群組規模和相應增長軌跡的錯誤估計[78]。此外,由于缺乏足夠的實質性信息來識別群組,模型可能無法正確識別樣本量較小的群組。在此情況下,軌跡的識別可能基于異常值或其他隨機波動,而不是真實的群組[22,36,79]。因此,研究人員應提供每個模型中各潛類別下樣本量的相關信息(具體操作過程請參閱表 2)。
條目 13:如果軌跡分析的目的是對個體進行分類,是否報告熵?
對個體進行分類是潛變量軌跡研究的常見分析目的,在這種情況下,研究人員必須報告分類的性能。評價分類性能的工具之一是相對熵值,該值越高表示個體歸類越準確。也就是說,模型能夠清晰地對特定類別中的個體進行分類,并且不同類別間存在足夠的區分度[78]。相對熵也被稱為衍生潛類別的“模糊性”度量[80,81]。當每個研究對象的所有后驗概率相等時,相對熵值為 0(即在三個潛類別下,所有參與者被分到其中一個潛類別的后驗概率為 0.33)。當每個參與者僅完全適合一個潛類別時相對熵為最大值 1,表示潛類別間能完全區分開來。因此,當熵值過低時需要小心,這提示研究對象沒有很好地被分類或沒有被分配到合適的潛類別。綜上,Celeux 等[58]提出,相對熵可被視為評估潛變量軌跡模型劃分數據效能的度量,Greenbaum 等[82](第 233 頁)對此進行了更為完善的解釋。然而,相對熵并不適用于確定潛類別數量[80,83,84]。Ram 等[85]建議,在多個模型的擬合指數(如,BIC)近似時,較高熵才對模型選擇有意義。盡管如此,我們仍建議作者報告熵值(見表 2)或像 Greenbaum 等[82](第 233 頁)一樣報告每個模型中的錯分數量。
條目 14a:是否報告最終結果的估計平均軌跡圖?
條目 14b:是否報告每個模型的估計平均軌跡圖?
如前所述,許多研究人員單獨使用實質性論據或結合模型選擇工具來決定潛類別數量。檢查軌跡圖對評估不同潛類別估計結果下的模型效能十分有幫助。需要報告的第一類圖為平均軌跡,不僅局限于最終模型,而應覆蓋所研究的每個模型(如在建模和評估分析結果階段均應進行模型比較)。我們在 https://osf.io/vw3t7/中提供了一個示例。因可能有大量模型需要擬合,報告全部軌跡圖存在一定挑戰性,但如果僅根據理論論證來決定類別數量,則必須報告所有估計結果的軌跡圖。需注意的是,若期刊不允許在正文中呈現較多的圖,可將該信息作為在線補充材料。我們認為,必須提供完整的軌跡圖信息以便其他研究者可重現最終分類數量。
條目 14c:是否報告最終模型的估計均值和每個潛類別下實際觀測到的個體軌跡圖?
除報告每個模型的估計平均軌跡外,結合實際觀測到的個體軌跡分析最終估計平均軌跡也十分重要。Erosheva 等[44]提出,通過上述圖示可直觀地看到潛變量群體軌跡對個體差異的解釋程度,及不同組別下實際觀測到的個體重疊程度。如圖 3 所示,所有個體可能都遵循平均軌跡且可能采用了 LCGA(圖 3a)。需注意,盡管該圖展示了個體軌跡的變化,但隨時間推移它們基本上都遵循相同的增長模式。但圖 3b 中個體軌跡差異較大,平均軌跡并未反映數據的真實情況。圖 3c 中,實際上沒有一個個體軌跡遵循平均軌跡,那么即使有足夠的擬合統計量,對結果的可解釋性也存在一定質疑。圖 3d 的情況更不理想,因為其中的二次效應完全可能是缺失數據所致。
 圖3
基于模擬數據的個體軌跡圖及估計均值
圖3
基于模擬數據的個體軌跡圖及估計均值
條目 15:是否用數字描述了最終潛類別模型的特征?
不僅需要呈現各模型下的潛變量軌跡圖,還需要呈現最終模型和每個模型各項參數的表格。具體包括:估計均值、標準差、P值、可信區間及用于估計每個模型參數的樣本量(注意任何缺失數據)。表格中的所有信息均應有助于讀者解讀結果,即使數據結果未在正文中完整報告,讀者仍應可獲得完整的模型結果。包含全部模型結果的表格還有助于實現結果報告的充分透明和完整重復。
條目 16:是否提供程序語句文件?
人們越來越意識到公開和透明的研究對維持和提高科學質量至關重要[86-90]。實現研究透明化的方式之一是共享數據、程序語句和其他支持材料(請參閱 Open Science Framework,https://osf.io/vw3t7/)。這些共享內容是所有論文的重要組成部分,它們讓其他研究人員可重現或改變論文中所報告的數據分析。此外,它們可使其他研究人員發現分析中的潛在錯誤,甚至是假的結果。公開程序語句文件是邁向完全公開數據和其他材料的第一步。多種方法可為讀者提供語句文件:如以附錄的形式呈現、通過在線補充材料或在線數據存儲庫來提供。語句信息最好不要僅在個人網站上展示(因為個人網站不是永久性的,可能會在某天關閉)。此外,一些新工具可助力語句的可及性。例如由 Center for Open Science 開發的在線協作工具,研究團隊可通過該工具將其研究材料的任一部分公開,以支持開放交流。Center for Open Science 還創造了一些“徽章”來證明論文滿足了開放材料要求。這些發展提示程序語句文件不應遠離讀者。我們的文件可在 Open Science Framework(https://osf.io/vw3t7/)上找到。
3 GRoLTS 在潛變量軌跡研究系統評價中的應用
為評估 GRoLTS 的一致性、有效性和可用性,我們利用 38 篇使用潛變量軌跡分析(即 LGMM 或 LCGA)來評估創傷事件后 PTSS 變化的研究對該報告規范進行了測試。每篇文章的平均評估所需時間為 20 分鐘,每篇論文評價由兩名評價員獨立進行。當得分相互矛盾時,評價員在快速陳述各自打分理由后,很容易便能達成共識。參考文獻的完整列表和相關細節請參閱 Open Science Framework(https://osf.io/vw3t7/)。
圖 4 展示了所有論文的 GRoLTS 總分,沒有一篇論文接近最高分 21 分(均值±標準差:9.47±1.97 分,范圍:5~15 分)。在檢查了具體的 GRoLTS 條目后(圖 5),我們發現一些條目在所有論文中幾乎都報告過,而有些條目幾乎從未報告過。我們將重點介紹最常報告和最少報告的前六個條目。
 圖4
38 個采用潛變量軌跡分析探討創傷性應激癥狀發展的研究的 GRoLTS 總分
圖4
38 個采用潛變量軌跡分析探討創傷性應激癥狀發展的研究的 GRoLTS 總分
 圖5
文章報告各項 GRoLTS 條目的比例
圖5
文章報告各項 GRoLTS 條目的比例
LGMM:潛變量增長混合模型;LCGA:潛類別增長分析;系統評價納入文章數量
3.1 最常報告的六大條目
3.1.1 條目 14a
所有文獻都提供了最終模型的估計平均軌跡圖(條目 14a)。
3.1.2 條目 10
幾乎所有文獻(97%)都報告了使用的模型選擇工具(條目 10),尤其是 BIC。約 2/3 文章還提到了其他模型選擇工具:SS-BIC 占 60.5%,AIC 占 63.2%,LRT 占 65.8%,BLRT 占 60.5%。12 篇文獻中提到模型擬合指數不一致,9 篇文獻中 AIC 或 BIC 不斷降低,10 篇文獻中基于統計標準的最優模型沒有意義,5 篇文獻中最佳模型中的一個類別僅覆蓋幾個人。一些文獻在模型選擇工具方面沒有提供簡單的潛類別估計結果,13 篇文獻僅根據理論而不是統計值來選擇模型。
3.1.3 條目 5
95% 的文獻報告了所用軟件(條目 5),其中 Mplus 最為常用(29 篇論文),其次是 SAS Proc Traj(7 篇文獻);30 篇文獻(79%)還報告了所用軟件版本。
3.1.4 條目 13
95% 的文獻報告了熵水平(條目 13),其熵值的中位數為 0.85。
3.1.5 條目 3c
89.5% 的文獻報告了如何處理缺失數據(條目 3c)。處理缺失數據最常用的方法為完整信息 ML(24 篇論文):但其中只有 1 項研究將這種方法與輔助變量相結合,3 項研究表明使用 MI 處理缺失數據。
3.1.6 條目 8
86% 的文獻對協變量(條目 8)進行了清晰描述。15 篇文獻使用了一步法,14 篇文獻使用了標準三步法(即分別保留最可能的類別成分與分析數據),只有 3 篇文獻使用了最近提出的 Vermunt 調整錯分三步法。
3.2 最少報告的六大條目
3.2.1 條目 14b/14c
沒有一篇 PTSS 文獻具體展示了每個模型的軌跡圖(條目 14b),僅有 5 篇文獻(13%)報告了最終估計平均軌跡與觀測到的個體軌跡(條目 14c)。但未報告此類軌跡圖(條目 14b 和 14c)并不局限于 PTSS 研究,在 Piquero[6]和 Erosheva[44]等人的系統評價中,分別發現 87 篇中有 0 篇、200 篇中僅有 8 篇(4%)軌跡研究報告了軌跡圖。
3.2.2 條目 6b
無一篇文獻報告了組間方差-協方差矩陣結構(條目 6b)。雖然從統計學角度來看組間方差-協方差矩陣結構十分重要,但顯然研究人員認為使用統計分析軟件默認的設置即可。
3.2.3 條目 9
僅有 1 個研究報告了所用的確切起始值數量(條目 9)。
3.2.4 條目 16
僅有 2 篇文獻中報告了公開程序語句文件(條目 16)。
3.2.5 條目 3a
僅有 2 篇文獻報告了缺失數據機制(條目 3a),且機制為 MAR。
3.2.6 條目 2
僅有 3 篇文獻報告了時間的變異性(條目 2)。
4 實例解讀
本節以美國西北大學的 Lloyd-Jones 等開展的一個隊列研究(coronary artery risk development in young adults study,CARDIA)[91]的縱向軌跡分析結果為例,利用 GRoLTS 清單進行評價,見表 3。
該文章于 2019 年 11 月發表在JAMA Cardiology,主要研究目的是探討從幼年到成年的 20 年間的蛋白尿軌跡與超聲心動圖測量的心肌結構和功能的關系,采用尿白蛋白與肌酐比值(urine albumin-to-creatinine ratio,UACR)測量蛋白尿的水平。
總體而言,針對 GRoLTS 清單的 21 個條目,該文章有 8 個條目未報告,有 2 個條目報告不充分,評分為 12 分。雖然原作者在文章的方法學部分較為詳細地描述了統計分析方法,但在結果部分的報告不太充分。
5 討論
本研究所制訂的 GRoLTS 是一種報告潛變量軌跡研究的工具(LGMM 或 LCGA)。研究者按照系統化的制訂流程,遵循專家小組和高級研究人員的意見,確定了報告軌跡研究結果必要的關鍵條目。無論文獻使用了何種統計模型,相應的報告規范都十分重要。其他報告規范,如隨機對照試驗報告的 CONSORT 清單,已被成功地推廣和應用。有系統評價表明,使用諸如 CONSORT 之類的報告規范確實提高了報告質量[92]。在潛變量增長軌跡模型研究領域,報告規范是呈現模型結果時必須要遵守的組成部分,其結果解釋在很大程度上與模型范式和估計的相關要素密切相關。
研究者建議所有潛變量增長軌跡模型都按照 GRoLTS 進行報告,以促進研究結果的合理呈現。需注意,GRoLTS 并非旨在衡量論文本身的質量,而是評估潛變量軌跡模型關鍵問題的報告質量。GRoLTS 條目全面而簡潔,雖然 GRoLTS 內容較為詳細,但很多條目僅需通過在論文中增添一些句子或使用在線補充材料即可滿足。GRoLTS 可供準備提交稿件的作者使用,也可作為期刊審稿時對 LGMM 或 LCGA 研究的報告規范。由于 LGMM 或 LCGA 研究發展迅速且在不同領域中廣泛應用,因此 GRoLTS 應該定期更新和修訂,必要時應進行條目添加或刪除。據研究者了解,軌跡方法在不同領域、不同類型的研究問題間存在較大差異。因此,報告軌跡結果時,還需考慮是否有 GRoLTS 未涵蓋的其他要點。
研究者想以 Bauer[93](第 782 頁)的一句話結束本文:“我試圖解決的基本問題是這些模型(指 LGMM/LCGA 模型)是否有可能推動心理學的發展。我確信,如果這些模型繼續按照目前的方式使用,那么答案顯然是否定的……因此,我認為,除非分析背后的理論和數據都非常成熟,否則應避免直接使用 GMMs。否則,GMMs 在心理學研究中的應用可能偏離正確發展方向而走入死胡同。”
研究者同意 Bauer 的觀點,因過去這些模型的報告方式既不透明也不一致,難以產生可靠的、可重復的結果。如果所有相關領域的研究人員都具有扎實的理論基礎并形成使用 GRoLTS 規范報告的習慣,那么相信采用潛變量增長軌跡建模將會得到進一步發展,并成為應用統計學中最透明和最可重現的領域之一。
資助 van de Schoot R 和 Vermunt JK 分別得到了荷蘭科學研究組織的資助:NWO-VIDI-452-14-006 和 NWO-VICI-453-10-002。
致謝 感謝在德爾菲研究不同階段提供反饋意見的專家(按字母順序):Heather Armstrong、Daniel Bauer、George Bonanno、Jan Boom、Patrick Curran、Isaac Galatzer-Levy、Christian Geiser、Kevin Grimm、Joop Hox、John Hipp、Loes Keijsers、Lynda 和 Dan King、Todd Little、Gitta Lubke、Peter Lugtig、Katherine Masyn、BengtMuthén、Daniel Nagin、Karen Nylund、Cecile Proust-Lima、Quinten Raaijmakers、Jost Reinecke、Paula Schnurr、Geert Smid。
注釋
① 通過潛變量軌跡分析,我們采用基于個體的分析技術來估計隨時間推移發展的未觀測到的個體亞組潛分類[1]。為了估計軌跡潛分類,將傳統潛變量增長模型[2]與混合成分[3]相結合。潛變量增長模型的基本思想是假設所有個體都來自同一個人群。當結合混合模型時,假設增長參數(截距、斜率等)在預先指定和未觀測到的亞人群間是變化的。這可通過使用分類潛變量來實現,分類潛變量允許各組有單獨的增長軌跡,并為每個(未觀測到的)組產生單獨的潛變量增長模型,每個模型都有其獨特的一組增長參數。
② 當小規模的潛類別是研究目標時最好選擇貝葉斯估計,其在小樣本 LGMM 和 LCGA 模型中的表現優于 ML 估計[78]。
③ 類別區分度指的是不同潛類別在統計上或實質上的差異。類別區分度可基于多種不同的軌跡特征,包括具有明顯區別的截距或斜率、不同的軌跡形狀(線性增長 vs. 非線性增長)、不同的潛變量增長因子協方差結構等[78]。
參考文獻
見原文。