危險比（risk ratio，RR）和風險比（hazard ratio，HR）是前瞻性研究中常用的效應指標。但在原始研究和 Meta 分析中描述效應量大小時不能交替使用，如何選擇合適的指標并正確解讀是臨床研究的關鍵。本文總結了效應指標中危險和風險的異同點，對比 RR 和 HR 在估計方法和臨床解讀之間的差異，并在同一研究中比較 RR 和 HR 的區別，并提供可行的轉換公式便于在 Meta 分析的合并中使用。
引用本文： 黃橋, 趙明娟, 羅麗莎, 鄧通, 曾憲濤, 王行環. 前瞻性研究中效應指標危險比（RR）和風險比（HR）的辨析與轉換. 中國循證醫學雜志, 2020, 20(10): 1221-1225. doi: 10.7507/1672-2531.202005092 復制
前瞻性研究是一種縱向研究設計，隨著時間推移，隨訪觀察僅在某一研究因素有所不同的相似個體，探究這一研究因素對研究結局（如死亡、腫瘤進展）發生的影響[1]。前瞻性研究可以確定暴露（干預）和結局之間的時序關系（暴露在前，結局在后），其在病因研究和腫瘤學研究中得到廣泛應用。前瞻性研究設計需要納入一組人群并進行較長時間隨訪，記錄的結局是事件結局（是否發生）或者時間-事件結局（持續時間、是否發生）。因涉及到 2 組或多組比較，常采用相對比作為效應指標。危險比（risk ratio，RR），又稱相對危險度（relative risk，RR），是前瞻性研究中以是否發生研究結局（如死亡）的效應指標，RR 表示的是兩個危險（risk）之間的比值[2]。風險比（hazard ratio，HR）是前瞻性研究中以時間-事件數據為結局的效應指標，表示的是兩個風險率（hazard rate）之間的比值。從臨床角度來講，危險和風險率均對應一種臨床結局，如死亡、腫瘤進展等。
RR 和 HR 作為效應指標在臨床研究中的應用越來越廣泛。因為二者都是相對比的指標，在解讀時，HR 常被錯誤地按照 RR 來進行臨床意義解讀，但兩者顯然不同，最明顯的區別是 HR 考慮事件發生時間的長短。Meta 分析制作的重要步驟之一是選擇合適的效應指標并嘗試進行 Meta 合并，如在偏態數據中不建議采用均數而是中位數進行合并[3, 4]。但當納入的同類研究分別匯報 HR 和 RR，如何選擇以及是否兩者可以轉換是 Meta 分析制作者常面臨的問題。臨床醫生或其他非統計領域的專家常因無法直觀理解兩者區別，導致采用的統計方法和效應指標使用不合理。因此，有必要對二者的聯系和區別進行系統性剖析，降低學習和使用的門檻。
筆者從危險和風險率入手，采用實例數據并可視化展示 HR 和 RR 之間的區別，方便研究者在進行原始研究和 Meta 分析時參考，同時引導 HR 和 RR 的正確和規范使用。
1 危險和風險率的對比
1.1 危險的計算
 |
危險表示隨訪到 t 時刻時，事件發生的概率，其中分子為到 t 時刻時新發事件累積人數，分母為隨訪開始時的總人數（公式 1）。因按照觀察時間累積，又可稱為累積危險或累積發生率，大小一般介于 0 到 1 之間。若隨訪時間足夠長，且入組人群均有發生事件的可能（如死亡），危險終將等于 1。因其分母為入組時總人數，所以危險的計算不允許刪失的出現。
1.2 風險率的計算
 |
 |
風險率，又稱風險，表示已生存到時間 t 的人群在 t 時刻時的單位時間事件發生率。分子為條件概率［P（A|B）表示在 B 條件下 A 事件發生的概率］，其表示為［
時間段的發生事件人數除以 t 時刻時仍生存的人數，分母為事件間隔 
（公式 2 和 3）。風險率是概率與時間相除所得的單位時間概率，其大小與時間單位有關。此外，風險率是求極限所得的值，當 
無限接近 0 時，時間范圍［
將無限接近 t 這一瞬間，所以風險率表示 t 時刻瞬間的單位時間概率。
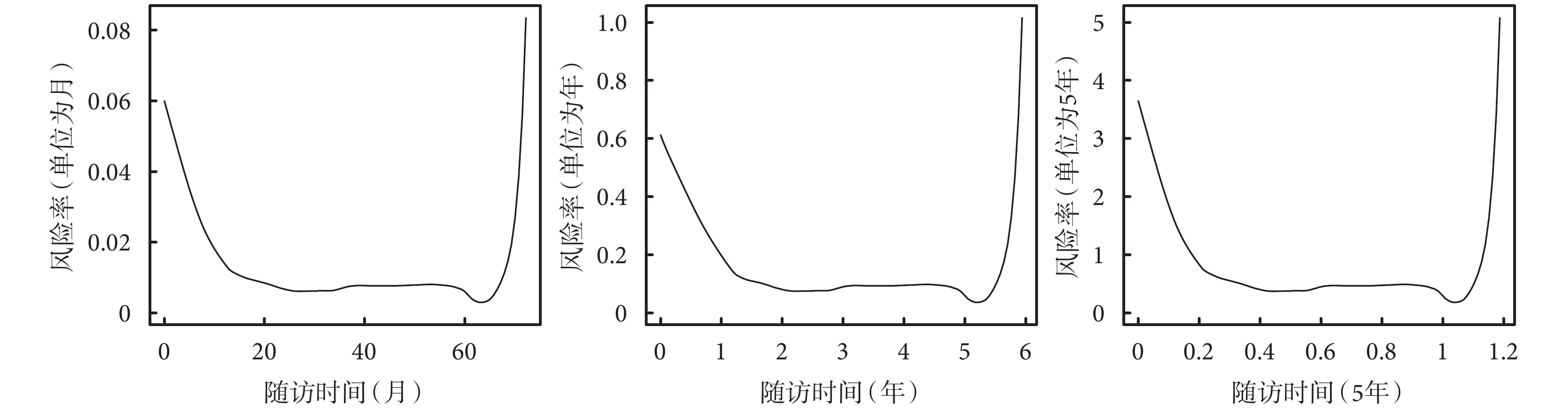
以伍斯特心臟病研究（Worcester Heart Attack Study）的公開數據為例[5]，采用不同的時間單位（月、年和五年）分別計算風險率，可以發現風險率隨著時間變化，變化趨勢完全一致，但是其大小卻不同，時間單位越大，風險率越大，范圍為［0，+∞），見圖 1。因風險率的條件概率計算中，分母僅考慮 t 時刻仍生存的人數，而不是入組時的總人數，所以計算允許刪失的存在。
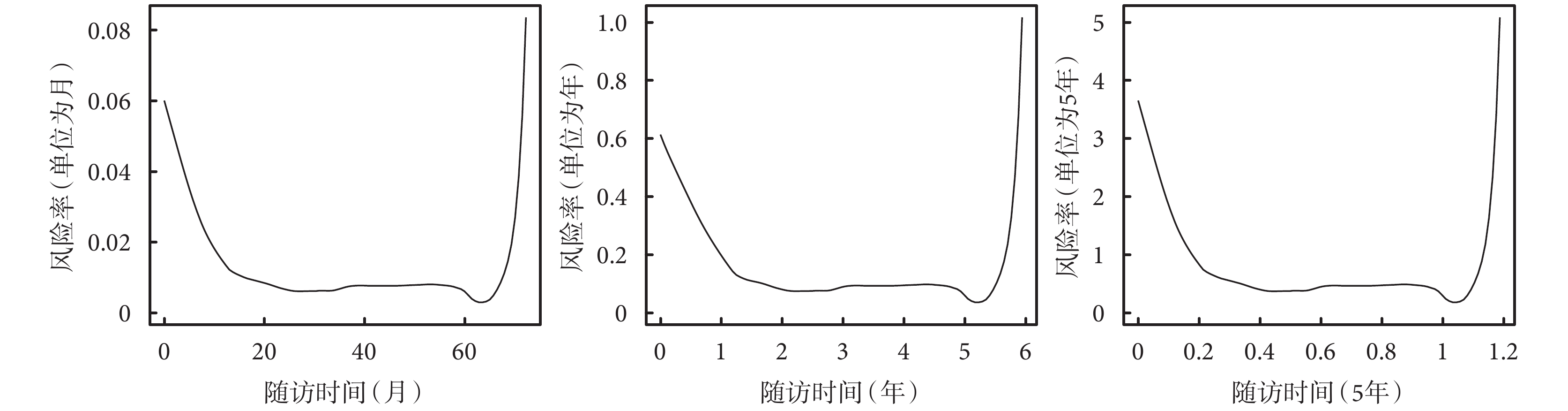圖1
相同數據中不同時間單位的風險率估計
1.3 危險和風險率的比較
危險和風險率的總結對比見表 1。
表1
危險和風險率的比較
2 RR 和 HR 的估計和臨床解讀
2.1 RR 的計算
 |
RR 是兩組危險的比值（公式 4）。將數據匯總成四格表的形式，分別計算暴露組（干預組）和對照組的危險，然后簡單計算比值可得到粗 RR。然而，在臨床研究中，混雜因素的存在可能會扭曲暴露與結局之間的關系，所以常需要采用高階統計方法控制混雜因素的影響。根據不同類型可以分為以下 4 種。
2.1.1 基于四格表拓展
第一種為分層 Mantel-Haenszel 法，該方法只允許納入為分類變量的混雜協變量，且個數不能太多，否則可能會出現四格表的單元格為 0 的情況，而無法計算。第二種使用 logistic 回歸計算各組的傾向得分，然后為平衡組間混雜因素進行匹配，根據匹配后的數據重新整理四格表計算 RR，該方法對樣本量要求較高[6]。
2.1.2 基于 logistic 回歸
第一種方法是通過多因素 logistic 回歸計算調整后的比值比（odds ratio，OR），然后根據公式轉換成 RR。一般來說當對照組的事件發生率小于 10% 時，RR 和 OR 的值接近[2]；第二種方法基于邊際概率，建立多因素 logistic 回歸模型，先假設所有個體為暴露組，估計每個觀測的預測概率后計算平均值（
），然后假設所有個體為非暴露組，估計預測概率后計算平均值（
），兩者的比值即為 RR，其置信區間估計需要采用 Bootstrap 法[1]。
2.1.3 基于離散變量分布的回歸
第一種為 Log-binomial 回歸，模型左邊為 ln（p），其中 p 為事件發生率，屬于是廣義線性模型的一種特殊類型，常應用于隊列研究和干預性研究中[7, 8]。因為因變量 ln（p）始終≤0，所以在使用該方法時可將截距設置為?4，提高模型擬合的成功率[9]。另外一種方法是采用穩健誤差方差估計的泊松回歸（Poisson regression with robust error variance），在泊松回歸中不采用穩健的誤差的方差估計時，置信區間估計保守。Zou 等[10]引入穩健的“三明治”方差估計方法改進泊松回歸，從而得到 RR 的穩健估計。
2.1.4 基于 Cox 等比例風險回歸
第一種用于估計指定時間的 RR，與基于 logistic 回歸的第二種方法類似。建立多因素 Cox 回歸模型，先假設所有個體為暴露組估計每個觀測在預測概率，計算指定時間概率的平均值（
），同樣操作計算對照組的平均值（
），兩者的比值即為 RR，置信區間估計采用 Bootstrap 法[11]。第二種是修正的 Cox 等比例風險回歸，將所有的觀測時間設置為相等的常數（特定時間），采用 Breslow 或 Efron 等的“結”處理方法修正 Cox 比例風險模型，估計 RR 及其置信區間[12]。
郜艷暉等[13]對 RR 和患病率比（prevalence ratio，PR）的估計方法進行了系統全面的介紹。Fang[14]使用 SAS 軟件實現了以上介紹的 8 種方法，并用實例展示各自的優缺點。對于非統計專家來說，從實用和便捷的角度出發，推薦先采用截距設置為負的 Log-binomial 回歸模型，若模型無法擬合時，則采用穩健誤差方差估計的泊松回歸。
2.2 HR 的計算
 |
HR 是兩組風險率的比值（公式 5）。各組的風險率需要在不同的隨訪時間點求極限，無法通過簡單的四格表計算。相較于參數生存回歸，Cox 等比例風險模型因不依賴特定的分布（如參數生存分析中的指數分布等）且無需估計基線風險率，廣泛應用于生存分析中的 HR 估計。在臨床研究中，常采用單因素的 Cox 等比例風險模型估計粗 HR，多因素模型估計調整后 HR。在進行 Cox 等比例風險模型前，需要進行等比例風險的假設檢驗。等比例風險是指盡管風險率隨著時間任意變化，但兩組的風險率之比在隨訪期間是恒定不變的。
2.3 臨床解讀
以一個干預性的隨機對照試驗為例，設置干預組和對照組，記錄結局事件為疾病進展，隨訪 5 年，同時估計 RR 和 HR。RR=1.5，表示干預組的 5 年疾病進展發生率是對照組的 1.5 倍（或者干預組的 5 年疾病進展發生率比對照組高 50%）。HR=2，表示干預導致患者的疾病進展更快，在某個時間點尚未進展的患者中，干預組的患者在下一個時間點疾病進展的機會是對照組的 2 倍。
3 HR 和 RR 之間的關系
3.1 HR 固定時 RR 與 HR 之間的關系
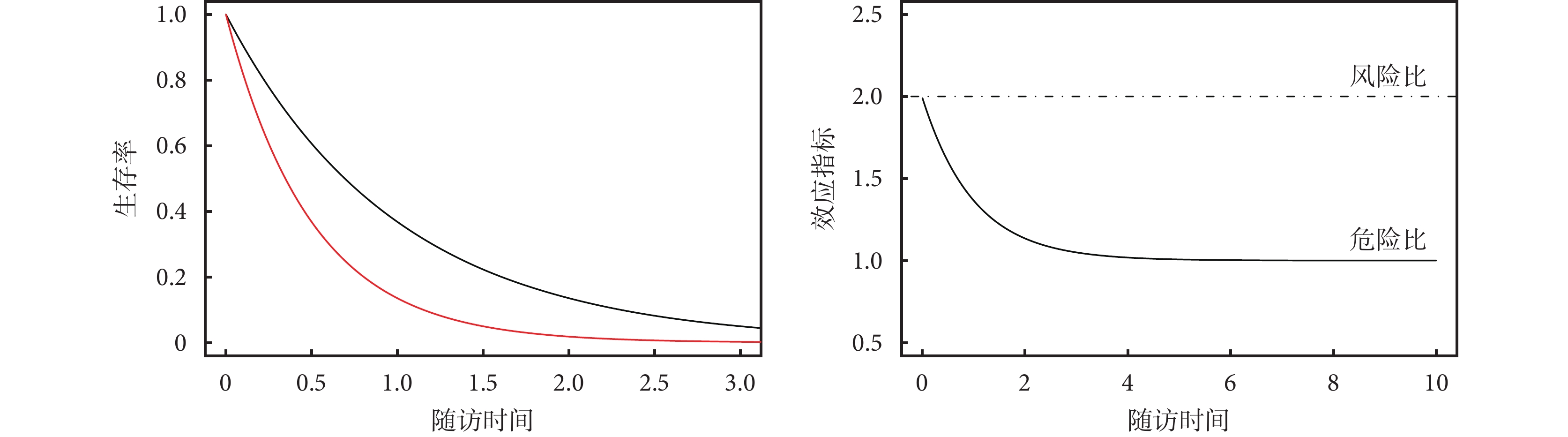
以最簡單的指數分布的參數生存分析為例，模擬原始時間-事件數據，HR 設置為 2，數據中不考慮刪失，繪制 Kaplan-Meier 曲線（圖 2），計算不同隨訪時間點的 RR，將 HR 和 RR 繪制在同一圖中（圖 2）。從圖中可見，僅在隨訪初期時，HR 與 RR 接近，在后期 RR 逐漸接近 1。
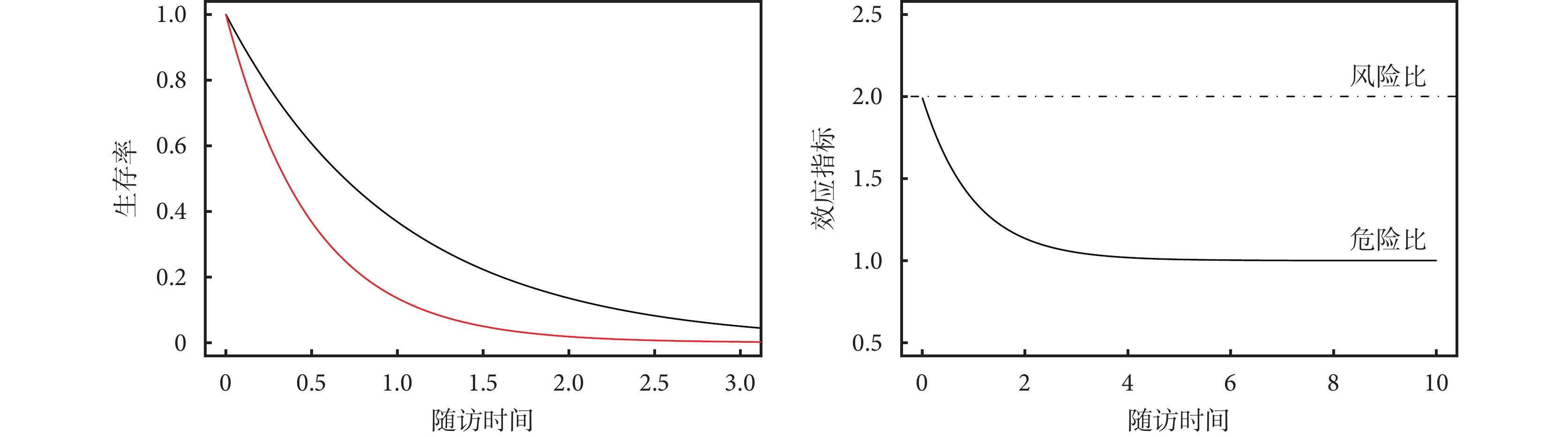圖2
指數分布的生存曲線中 HR 和 RR 之間關系
3.2 RR 固定時 HR 與 RR 之間的關系
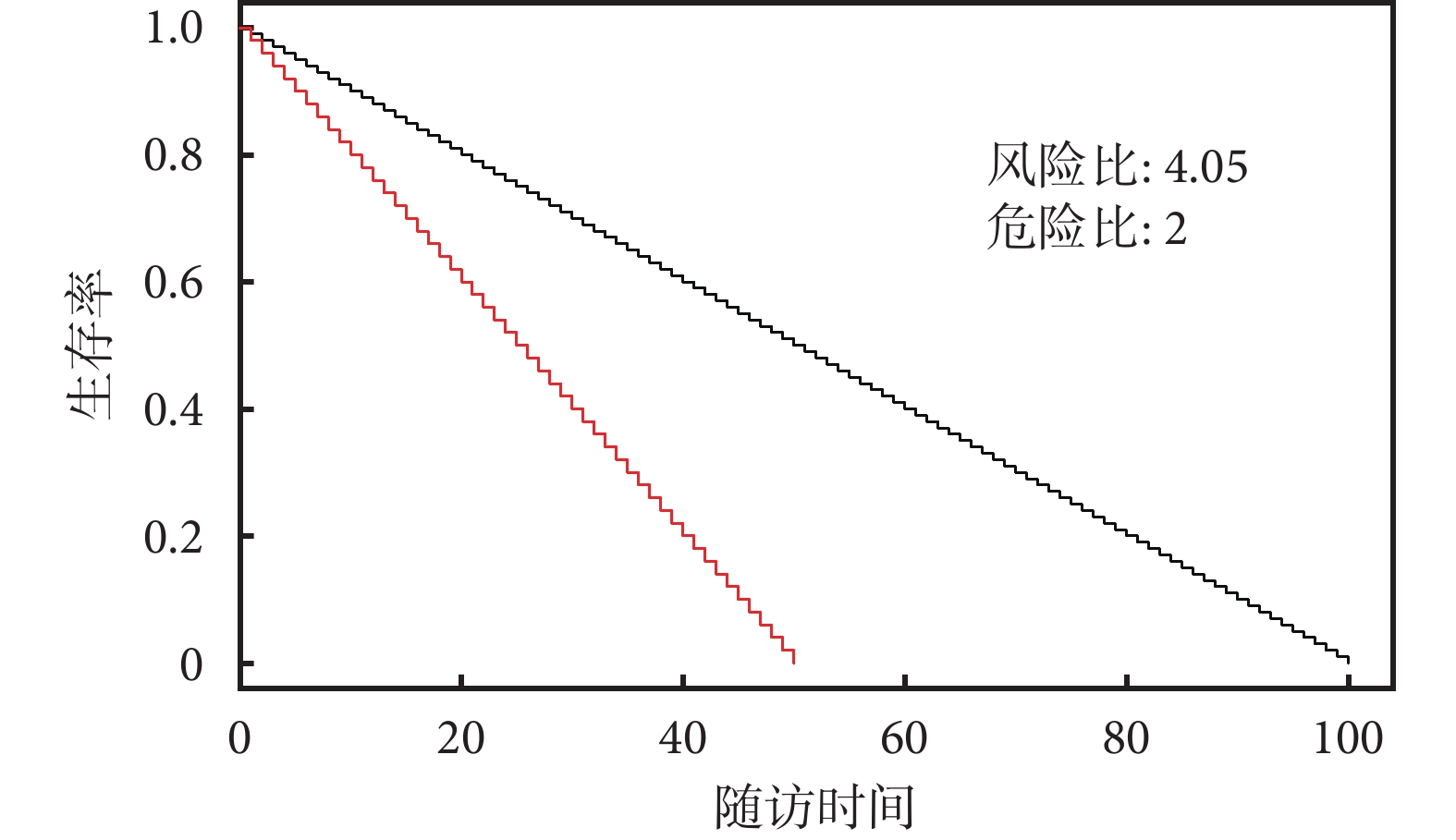
假設試驗組和對照組均納入 100 人進行隨訪，在每個單位時間，試驗組有 2 人死亡，對照組有 1 人死亡，直到所有對象都發生事件。此時 RR 恒等于 2，采用 Cox 等比例風險模型估計的 HR 為 4.05（圖 3）。
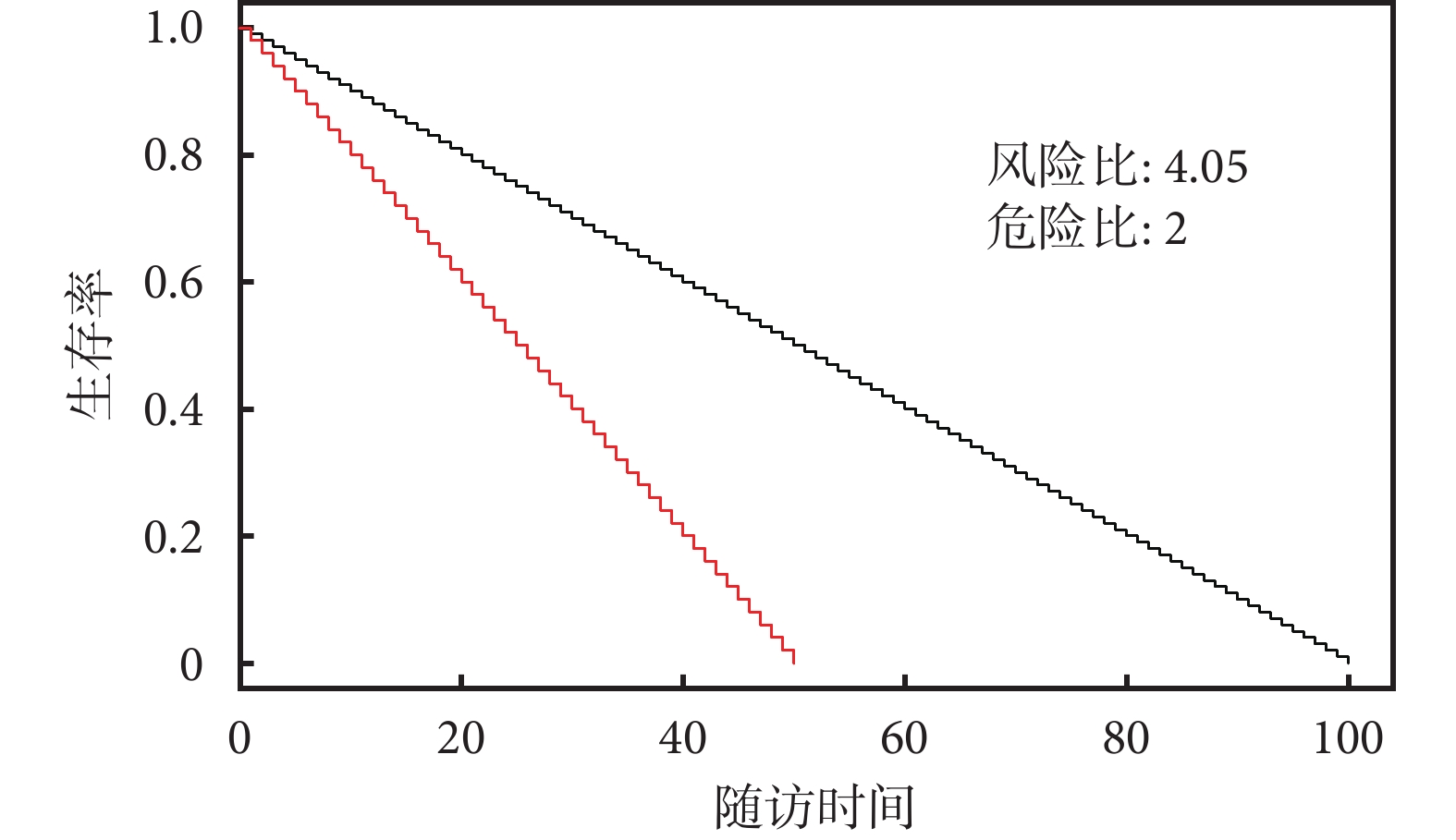圖3
RR固定時生存曲線中 HR 和 RR 之間的關系
3.3 HR 與 RR 的轉換
HR 在隨訪期間恒定為 k 時，RR 并不為 k，且 RR 可能隨著時間變化。為理解 HR 和 RR 不等，如以死亡為結局，若 HR 恒定不變，因每個人最終均會死亡，RR 最終將逐漸接近 1。在 Meta 分析中，HR 和 RR 作為效應指標得到廣泛使用。若 Meta 分析納入的研究同時使用 HR 和 RR 時，建議按不同的指標分亞組進行 Meta 合并。但納入文獻較少不適合分亞組時，則可以嘗試將 HR 轉化為 RR 后進行合并。
若能獲得隨訪結束時對照組的事件發生率 P0，可采用公式 6 將 HR 轉換成 RR[15]。若關注的結局事件在隨訪期間能必然發生時，該公式滿足 RR 在隨訪期間逐漸趨近 1 的特性，當 P0=1 時，RR=1。
 |
國外學者 VanderWeele[16]提出在滿足等比例風險的情況下，采用公式 7 進行 HR 和 RR 之間的近似轉換。若兩組的事件發生率介于 0.2 到 0.8，轉換的誤差小于 16%；但如果不滿足此條件，轉換導致的偏差可能高達 80%。
 |
2019 年 12 月，VanderWeele 發表了將轉換 HR 為 RR 的進一步研究結果[17]。首先，定義暴露組和對照組事件發生率分別為 P1 和 P0，且兩者大小介于［w，u］，采用基于最優偏差比的最大最小值轉換（optimal bias-ratio minimax conversion），進一步減少轉換帶來偏差。根據 HR 和 1 的關系，分為以下兩者情況。
若 HR>1，則定義 w≤P0≤P1≤u，
 |
若 HR<1，則 w≤P1≤P0≤u，
 |
同樣的，若兩組的事件發生率介于 0.2 到 0.8，轉換的誤差相較于公式 7 進一步降低，小于 13%[17]。概率區間［w，u］的設置會影響轉換的結果，若 P0 和 P1 的合理范圍的信息不足，公式 8 和 9 的轉換可能存在問題，此時可采用公式 7 轉換。
由樣本推斷總體時，因存在抽樣誤差，效應指標常需結合點估計值（HR 或 RR）及其 95% 置信區間表示。在進行置信區間的轉換時，可依次將區間的上限和下限帶入公式，計算轉換后的置信區間。例如，某研究的效應量為 HR=1.14［95%CI（1.08，1.21）］，采用公式 6 可以轉換得到近似的 RR 值，RR=1.13［95%（1.08，1.20）］。
4 總結
RR 和 HR 作為前瞻性研究中常用的效應指標，RR 主要關注結局事件是否發生，HR 主要關注幸免于結局事件的時間長短，二者不同，描述效應大小時不能交替使用。本文從基本概念上對比了 RR 和 HR，對 RR 和 HR 的常用統計分析方法進行分析，以實例區分二者在臨床結果上的表達，最后采用模擬數據對比 RR 和 HR 的大小，并提供可能的轉換工具。正確理解 RR 和 HR 的聯系和區別，將有助于臨床研究者進行恰當的統計分析、結果表達和文獻解讀。
前瞻性研究是一種縱向研究設計，隨著時間推移，隨訪觀察僅在某一研究因素有所不同的相似個體，探究這一研究因素對研究結局（如死亡、腫瘤進展）發生的影響[1]。前瞻性研究可以確定暴露（干預）和結局之間的時序關系（暴露在前，結局在后），其在病因研究和腫瘤學研究中得到廣泛應用。前瞻性研究設計需要納入一組人群并進行較長時間隨訪，記錄的結局是事件結局（是否發生）或者時間-事件結局（持續時間、是否發生）。因涉及到 2 組或多組比較，常采用相對比作為效應指標。危險比（risk ratio，RR），又稱相對危險度（relative risk，RR），是前瞻性研究中以是否發生研究結局（如死亡）的效應指標，RR 表示的是兩個危險（risk）之間的比值[2]。風險比（hazard ratio，HR）是前瞻性研究中以時間-事件數據為結局的效應指標，表示的是兩個風險率（hazard rate）之間的比值。從臨床角度來講，危險和風險率均對應一種臨床結局，如死亡、腫瘤進展等。
RR 和 HR 作為效應指標在臨床研究中的應用越來越廣泛。因為二者都是相對比的指標，在解讀時，HR 常被錯誤地按照 RR 來進行臨床意義解讀，但兩者顯然不同，最明顯的區別是 HR 考慮事件發生時間的長短。Meta 分析制作的重要步驟之一是選擇合適的效應指標并嘗試進行 Meta 合并，如在偏態數據中不建議采用均數而是中位數進行合并[3, 4]。但當納入的同類研究分別匯報 HR 和 RR，如何選擇以及是否兩者可以轉換是 Meta 分析制作者常面臨的問題。臨床醫生或其他非統計領域的專家常因無法直觀理解兩者區別，導致采用的統計方法和效應指標使用不合理。因此，有必要對二者的聯系和區別進行系統性剖析，降低學習和使用的門檻。
筆者從危險和風險率入手，采用實例數據并可視化展示 HR 和 RR 之間的區別，方便研究者在進行原始研究和 Meta 分析時參考，同時引導 HR 和 RR 的正確和規范使用。
1 危險和風險率的對比
1.1 危險的計算
|
危險表示隨訪到 t 時刻時，事件發生的概率，其中分子為到 t 時刻時新發事件累積人數，分母為隨訪開始時的總人數（公式 1）。因按照觀察時間累積，又可稱為累積危險或累積發生率，大小一般介于 0 到 1 之間。若隨訪時間足夠長，且入組人群均有發生事件的可能（如死亡），危險終將等于 1。因其分母為入組時總人數，所以危險的計算不允許刪失的出現。
1.2 風險率的計算
|
|
風險率，又稱風險，表示已生存到時間 t 的人群在 t 時刻時的單位時間事件發生率。分子為條件概率［P（A|B）表示在 B 條件下 A 事件發生的概率］，其表示為［時間段的發生事件人數除以 t 時刻時仍生存的人數，分母為事件間隔 （公式 2 和 3）。風險率是概率與時間相除所得的單位時間概率，其大小與時間單位有關。此外，風險率是求極限所得的值，當 無限接近 0 時，時間范圍［將無限接近 t 這一瞬間，所以風險率表示 t 時刻瞬間的單位時間概率。
以伍斯特心臟病研究（Worcester Heart Attack Study）的公開數據為例[5]，采用不同的時間單位（月、年和五年）分別計算風險率，可以發現風險率隨著時間變化，變化趨勢完全一致，但是其大小卻不同，時間單位越大，風險率越大，范圍為［0，+∞），見圖 1。因風險率的條件概率計算中，分母僅考慮 t 時刻仍生存的人數，而不是入組時的總人數，所以計算允許刪失的存在。
圖1
相同數據中不同時間單位的風險率估計
1.3 危險和風險率的比較
危險和風險率的總結對比見表 1。
表1
危險和風險率的比較
2 RR 和 HR 的估計和臨床解讀
2.1 RR 的計算
|
RR 是兩組危險的比值（公式 4）。將數據匯總成四格表的形式，分別計算暴露組（干預組）和對照組的危險，然后簡單計算比值可得到粗 RR。然而，在臨床研究中，混雜因素的存在可能會扭曲暴露與結局之間的關系，所以常需要采用高階統計方法控制混雜因素的影響。根據不同類型可以分為以下 4 種。
2.1.1 基于四格表拓展
第一種為分層 Mantel-Haenszel 法，該方法只允許納入為分類變量的混雜協變量，且個數不能太多，否則可能會出現四格表的單元格為 0 的情況，而無法計算。第二種使用 logistic 回歸計算各組的傾向得分，然后為平衡組間混雜因素進行匹配，根據匹配后的數據重新整理四格表計算 RR，該方法對樣本量要求較高[6]。
2.1.2 基于 logistic 回歸
第一種方法是通過多因素 logistic 回歸計算調整后的比值比（odds ratio，OR），然后根據公式轉換成 RR。一般來說當對照組的事件發生率小于 10% 時，RR 和 OR 的值接近[2]；第二種方法基于邊際概率，建立多因素 logistic 回歸模型，先假設所有個體為暴露組，估計每個觀測的預測概率后計算平均值（），然后假設所有個體為非暴露組，估計預測概率后計算平均值（），兩者的比值即為 RR，其置信區間估計需要采用 Bootstrap 法[1]。
2.1.3 基于離散變量分布的回歸
第一種為 Log-binomial 回歸，模型左邊為 ln（p），其中 p 為事件發生率，屬于是廣義線性模型的一種特殊類型，常應用于隊列研究和干預性研究中[7, 8]。因為因變量 ln（p）始終≤0，所以在使用該方法時可將截距設置為?4，提高模型擬合的成功率[9]。另外一種方法是采用穩健誤差方差估計的泊松回歸（Poisson regression with robust error variance），在泊松回歸中不采用穩健的誤差的方差估計時，置信區間估計保守。Zou 等[10]引入穩健的“三明治”方差估計方法改進泊松回歸，從而得到 RR 的穩健估計。
2.1.4 基于 Cox 等比例風險回歸
第一種用于估計指定時間的 RR，與基于 logistic 回歸的第二種方法類似。建立多因素 Cox 回歸模型，先假設所有個體為暴露組估計每個觀測在預測概率，計算指定時間概率的平均值（），同樣操作計算對照組的平均值（），兩者的比值即為 RR，置信區間估計采用 Bootstrap 法[11]。第二種是修正的 Cox 等比例風險回歸，將所有的觀測時間設置為相等的常數（特定時間），采用 Breslow 或 Efron 等的“結”處理方法修正 Cox 比例風險模型，估計 RR 及其置信區間[12]。
郜艷暉等[13]對 RR 和患病率比（prevalence ratio，PR）的估計方法進行了系統全面的介紹。Fang[14]使用 SAS 軟件實現了以上介紹的 8 種方法，并用實例展示各自的優缺點。對于非統計專家來說，從實用和便捷的角度出發，推薦先采用截距設置為負的 Log-binomial 回歸模型，若模型無法擬合時，則采用穩健誤差方差估計的泊松回歸。
2.2 HR 的計算
|
HR 是兩組風險率的比值（公式 5）。各組的風險率需要在不同的隨訪時間點求極限，無法通過簡單的四格表計算。相較于參數生存回歸，Cox 等比例風險模型因不依賴特定的分布（如參數生存分析中的指數分布等）且無需估計基線風險率，廣泛應用于生存分析中的 HR 估計。在臨床研究中，常采用單因素的 Cox 等比例風險模型估計粗 HR，多因素模型估計調整后 HR。在進行 Cox 等比例風險模型前，需要進行等比例風險的假設檢驗。等比例風險是指盡管風險率隨著時間任意變化，但兩組的風險率之比在隨訪期間是恒定不變的。
2.3 臨床解讀
以一個干預性的隨機對照試驗為例，設置干預組和對照組，記錄結局事件為疾病進展，隨訪 5 年，同時估計 RR 和 HR。RR=1.5，表示干預組的 5 年疾病進展發生率是對照組的 1.5 倍（或者干預組的 5 年疾病進展發生率比對照組高 50%）。HR=2，表示干預導致患者的疾病進展更快，在某個時間點尚未進展的患者中，干預組的患者在下一個時間點疾病進展的機會是對照組的 2 倍。
3 HR 和 RR 之間的關系
3.1 HR 固定時 RR 與 HR 之間的關系
以最簡單的指數分布的參數生存分析為例，模擬原始時間-事件數據，HR 設置為 2，數據中不考慮刪失，繪制 Kaplan-Meier 曲線（圖 2），計算不同隨訪時間點的 RR，將 HR 和 RR 繪制在同一圖中（圖 2）。從圖中可見，僅在隨訪初期時，HR 與 RR 接近，在后期 RR 逐漸接近 1。
圖2
指數分布的生存曲線中 HR 和 RR 之間關系
3.2 RR 固定時 HR 與 RR 之間的關系
假設試驗組和對照組均納入 100 人進行隨訪，在每個單位時間，試驗組有 2 人死亡，對照組有 1 人死亡，直到所有對象都發生事件。此時 RR 恒等于 2，采用 Cox 等比例風險模型估計的 HR 為 4.05（圖 3）。
圖3
RR固定時生存曲線中 HR 和 RR 之間的關系
3.3 HR 與 RR 的轉換
HR 在隨訪期間恒定為 k 時，RR 并不為 k，且 RR 可能隨著時間變化。為理解 HR 和 RR 不等，如以死亡為結局，若 HR 恒定不變，因每個人最終均會死亡，RR 最終將逐漸接近 1。在 Meta 分析中，HR 和 RR 作為效應指標得到廣泛使用。若 Meta 分析納入的研究同時使用 HR 和 RR 時，建議按不同的指標分亞組進行 Meta 合并。但納入文獻較少不適合分亞組時，則可以嘗試將 HR 轉化為 RR 后進行合并。
若能獲得隨訪結束時對照組的事件發生率 P0，可采用公式 6 將 HR 轉換成 RR[15]。若關注的結局事件在隨訪期間能必然發生時，該公式滿足 RR 在隨訪期間逐漸趨近 1 的特性，當 P0=1 時，RR=1。
|
國外學者 VanderWeele[16]提出在滿足等比例風險的情況下，采用公式 7 進行 HR 和 RR 之間的近似轉換。若兩組的事件發生率介于 0.2 到 0.8，轉換的誤差小于 16%；但如果不滿足此條件，轉換導致的偏差可能高達 80%。
|
2019 年 12 月，VanderWeele 發表了將轉換 HR 為 RR 的進一步研究結果[17]。首先，定義暴露組和對照組事件發生率分別為 P1 和 P0，且兩者大小介于［w，u］，采用基于最優偏差比的最大最小值轉換（optimal bias-ratio minimax conversion），進一步減少轉換帶來偏差。根據 HR 和 1 的關系，分為以下兩者情況。
若 HR>1，則定義 w≤P0≤P1≤u，
|
若 HR<1，則 w≤P1≤P0≤u，
|
同樣的，若兩組的事件發生率介于 0.2 到 0.8，轉換的誤差相較于公式 7 進一步降低，小于 13%[17]。概率區間［w，u］的設置會影響轉換的結果，若 P0 和 P1 的合理范圍的信息不足，公式 8 和 9 的轉換可能存在問題，此時可采用公式 7 轉換。
由樣本推斷總體時，因存在抽樣誤差，效應指標常需結合點估計值（HR 或 RR）及其 95% 置信區間表示。在進行置信區間的轉換時，可依次將區間的上限和下限帶入公式，計算轉換后的置信區間。例如，某研究的效應量為 HR=1.14［95%CI（1.08，1.21）］，采用公式 6 可以轉換得到近似的 RR 值，RR=1.13［95%（1.08，1.20）］。
4 總結
RR 和 HR 作為前瞻性研究中常用的效應指標，RR 主要關注結局事件是否發生，HR 主要關注幸免于結局事件的時間長短，二者不同，描述效應大小時不能交替使用。本文從基本概念上對比了 RR 和 HR，對 RR 和 HR 的常用統計分析方法進行分析，以實例區分二者在臨床結果上的表達，最后采用模擬數據對比 RR 和 HR 的大小，并提供可能的轉換工具。正確理解 RR 和 HR 的聯系和區別，將有助于臨床研究者進行恰當的統計分析、結果表達和文獻解讀。
