Meta 分析可定量、科學地整合研究結果,常用的兩種統計模型為固定效應模型和隨機效應模型,在實際運用中選擇合適的 Meta 分析合并模型非常重要。本文介紹經典 Meta 分析統計模型的新觀點,及其假設、結果解釋,探討合理選擇模型時應考慮的因素,并給出推薦建議。
Meta 分析可定量、科學地整合研究結果,已在許多科學領域取得顯著成果[1]。在醫學領域常可用于比較不同干預措施有益還是有害[2]。一般認為,經典 Meta 分析合并數據最主要的統計模型是固定效應(fixed-effect,FE)模型和隨機效應(random-effect,RE)模型[3, 4]。合理選擇 Meta 分析合并模型非常重要,在 Meta 分析實踐中,一些研究者首先選用 FE 模型,然后進行效應量的異質性檢驗(如,Q 統計量),若異質性檢驗無統計學意義,則認為 FE 模型適合于數據,宜采用 FE 模型分析;若異質性檢驗有統計學意義,則認為 FE 模型不適合于數據,宜采用 RE 模型分析[3]。但這類應當避免的模型選擇錯誤可影響整合研究結果的準確性,在第 6 版《Cochrane 干預措施系統評價員手冊》[5]明確指出:“決不應該根據異質性統計檢驗做出使用 FE 或 RE 模型的選擇”。因此,本文在復習文獻基礎上,介紹經典 Meta 分析統計模型的新觀點及其假設、結果解釋,探討合理選擇模型時應考慮的因素,以及如何合理選擇應用。
1 Meta 分析的基本原理
經典 Meta 分析是典型的二步過程,其基本原理是[5]:第一步,計算納入 Meta 分析的每個研究的統計量。用相同方法來描述每個研究干預的觀測效應量。第二步,通過對每個研究干預的觀測效應量進行加權取平均數來獲得總的合并干預效應。其公式為:
 |
式中, 為第 i 個研究中的干預效應(如,比值比對數、相對危險比對數、風險比對數、率差、均數差、標化均數差等效應量),
為第 i 個研究中的干預效應(如,比值比對數、相對危險比對數、風險比對數、率差、均數差、標化均數差等效應量), 為第 i 個研究的權重。
為第 i 個研究的權重。
從公式(1)可知,如果每個研究的權重相同,則加權平均數等于干預效應的平均值。
2 Meta 分析統計模型及其假設與解釋
經典 Meta 分析的統計模型對于計算和解釋 Meta 分析的結果非常重要,但由于 FE 和 RE 統計模型采用相似的公式計算統計量,有時可能得到相似的結果,以至常被誤認為兩個模型可相互替換使用。但實際上,不同模型基于不同假設,并且提供不同的參數估計值。
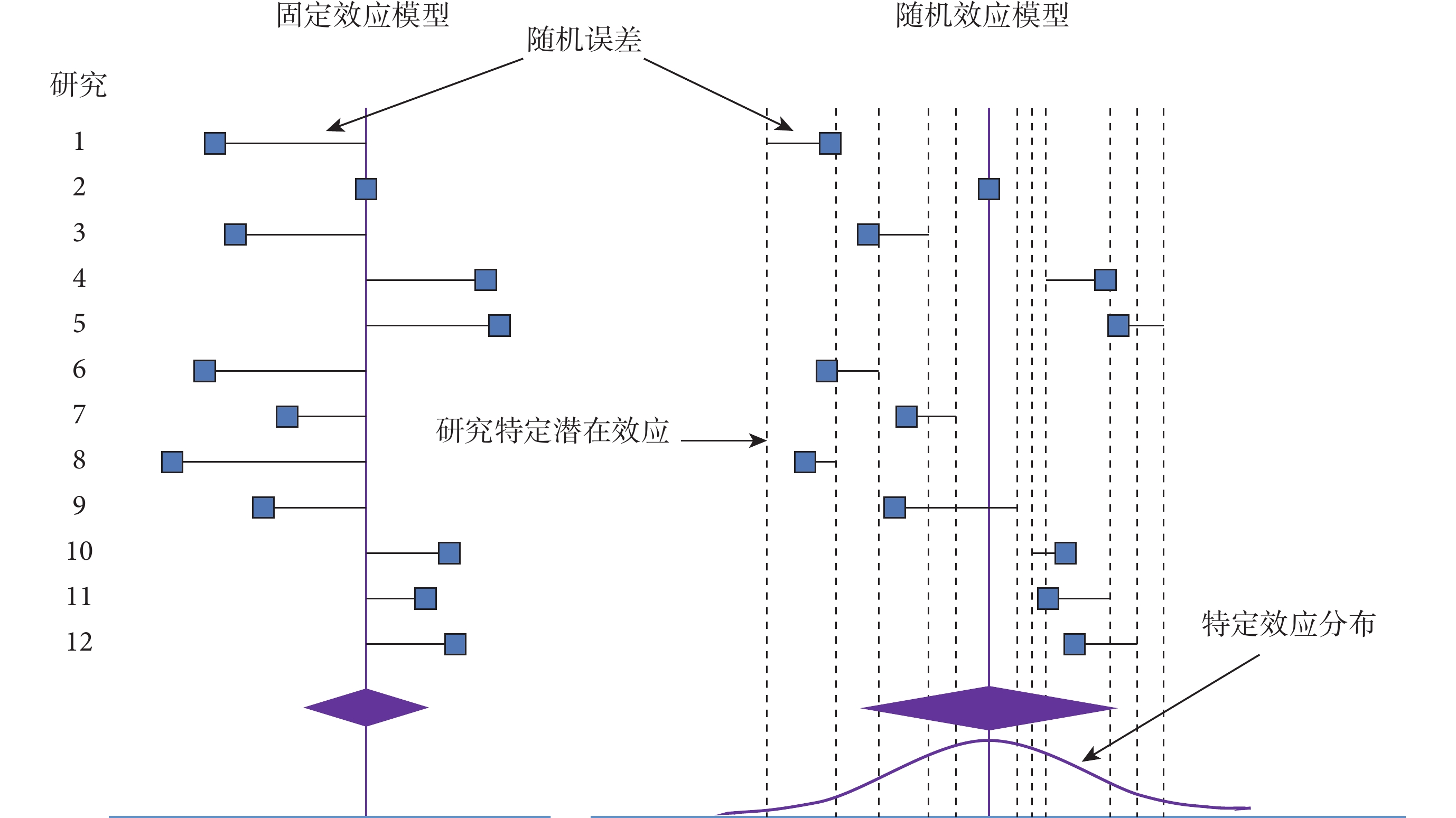
FE 模型[4, 6, 7]假設納入 Meta 分析的所有研究均有一個相同的干預效應(量級和方向均相同),不同研究的觀測效應量之間的差異均由抽樣誤差所示(如圖 1 左側部分所示)。合并效應量是研究特定效應量的加權平均數;每個研究分配到的權重等于研究內效應量方差的倒數;大樣本研究所占權重大幅度高于小樣本研究;研究的精度越大,對合并效應量的貢獻度就越大;故統計推斷有可能受到納入分析的樣本量影響。
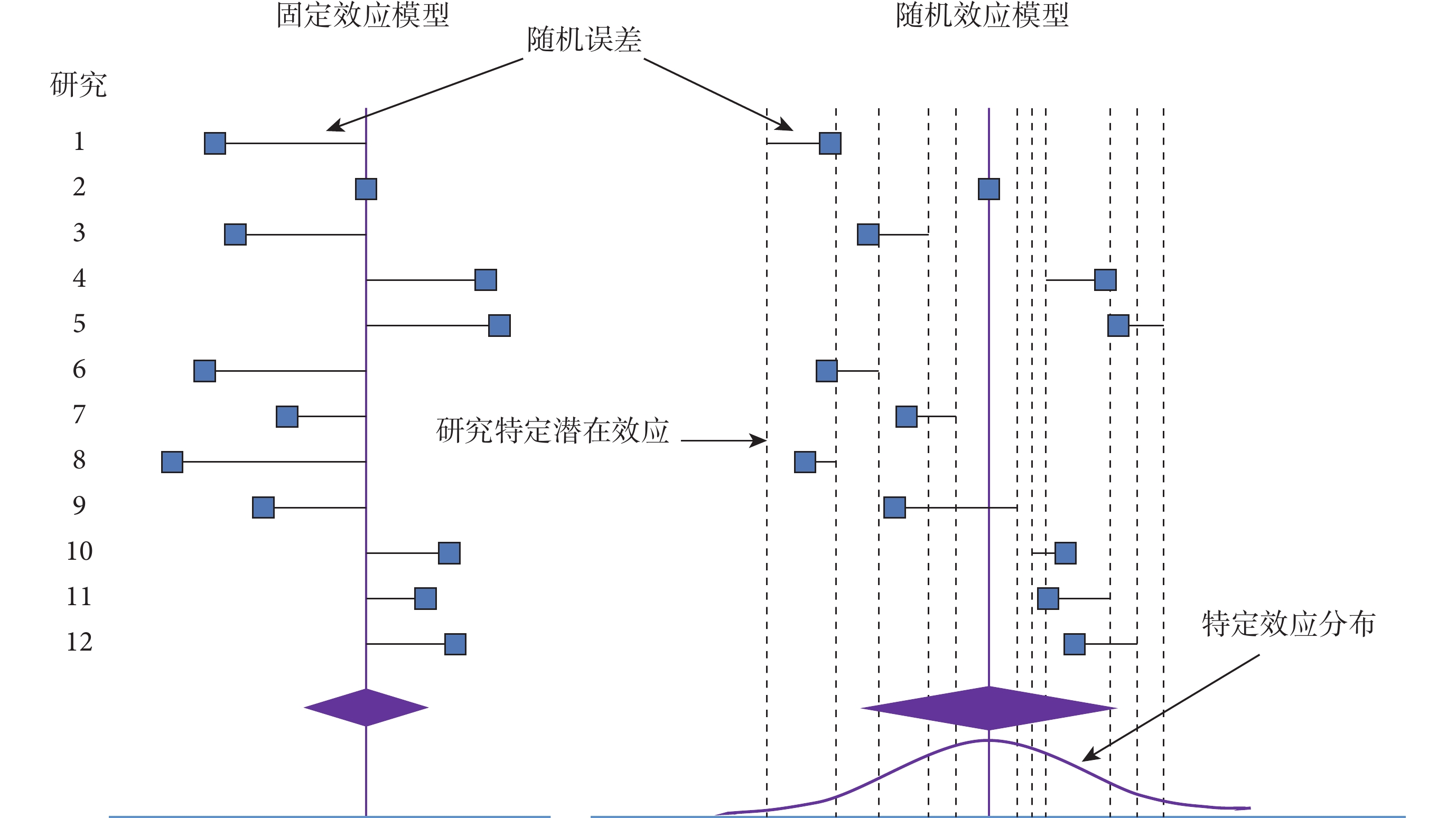 圖1
固定效應模型和隨機效應模型圖解(引自 Nikolakopoulou 等[6]的文獻)
圖1
固定效應模型和隨機效應模型圖解(引自 Nikolakopoulou 等[6]的文獻)
RE 模型[4, 6, 7]假設納入分析的研究間干預效應可以不同,觀測效應量的不同由隨機誤差和真實干預效應不同所致(圖 1 右則部分所示)。合并效應量是研究特定效應量的加權平均數;每個研究分配到的權重等于研究內效應量方差與研究間異質性方差和的倒數;大樣本研究占權重高于小樣本研究,但大樣本研究所占權重比在 FE 模型中小;對未來研究干預效應的預測更可靠;預測區間可表達真實效應量離散程度,可用于解釋單個研究真實效應量的預測范圍。
Bender[8]、Rice[9]等根據研究目的和假設等將 Meta 分析統計模型拓展為三個:共同效應(common-effect,CE)模型、FE模型和 RE 模型,請注意此處的 FE 模型與經典“FE 模型”的英文表達方式不同,在最新版 Stata 16.0 軟件中關于 Meta 分析的統計模塊采用的是這三種模型[10]。假設納入分析的第  (
( )個研究的觀測效應量為
)個研究的觀測效應量為  ,其相應方差為
,其相應方差為  ,真實效應量為
,真實效應量為  ,研究間異質性方差為
,研究間異質性方差為  ;描述第 i 個研究的抽樣誤誤差的隨機變量為
;描述第 i 個研究的抽樣誤誤差的隨機變量為  ,描述研究間異質性的隨機變量為
,描述研究間異質性的隨機變量為  ,合并效應量為
,合并效應量為  ,則三個模型的表達、假設、結果解釋等比較如表 1 所示,從中可以看出,Bender 等提出的 CE 模型和 FE 模型使用的加權平均統計量相同,因此所獲得的結果也相同。
,則三個模型的表達、假設、結果解釋等比較如表 1 所示,從中可以看出,Bender 等提出的 CE 模型和 FE 模型使用的加權平均統計量相同,因此所獲得的結果也相同。
3 不同模型的合理選擇依據和建議
Meta 分析中如何選擇統計模型,歷來存有爭議。不同的統計學家和臨床研究人員可能偏愛不同的統計模型[11],即使是第 6 版《Cochrane 干預措施系統評價員手冊》也未能提供權威的統一推薦意見[5]。筆者認為,應從統計模型假說、Meta 分析目的、納入 Meta 分析的研究數量和樣本量、研究間異質性、抽樣框架等不同方面綜合考慮來選擇合適的統計模型。
3.1 統計模型假說
如果假定納入 Meta 分析的研究具有共同的效應量,則可選用 CM 模型,但一般認為跨研究間干預效應完全相同是難以置信的(除非干預毫無效果)[5],這也是 CM 模型最主要的局限[8]。如果假定研究具有不同的干預效應,但效應量是“固定的”,則可選用 FE 模型;如果效應量是“隨機的”,則可選用 RE 模型。
3.2 Meta 分析目的
如果研究者的意圖僅僅是獲得納入 Meta 分析研究的干預效應平均值,則選用 FE 模型;如果研究意圖不僅僅是獲得納入 Meta 分析研究的干預效應平均值,而是要了解推廣應用到更為廣泛的人群的效應,則可選用 RE 模型[11, 12]。
3.3 研究數量和樣本量
納入 Meta 分析的研究數量足夠多時選擇 RE 模型,數量少時宜選擇 FE 模型[12]。雖然 RE 模型通常情況下是合適的模型,但當研究數量非常少( )時,因難以準確估計研究間方差,宜選擇 FE 模型[3, 11, 13]。特別是,當研究數量
)時,因難以準確估計研究間方差,宜選擇 FE 模型[3, 11, 13]。特別是,當研究數量  時,采用 CE 模型或 FE 模型,但更傾向于選擇 CE 模型,除非有違背 CE 模型假設的強假設[8]。但需要指出的是,即使是研究數量少(k=2~4)時,從技術上而言仍然可以評估異質性(如,采用貝葉斯方法),因為異質性評價是系統評價/Meta 分析的基本步驟。針對同一研究問題,當一項研究樣本量非常大且比其他的一個或多個小樣本研究結果更可靠時,選擇 FE 模型[11]。
時,采用 CE 模型或 FE 模型,但更傾向于選擇 CE 模型,除非有違背 CE 模型假設的強假設[8]。但需要指出的是,即使是研究數量少(k=2~4)時,從技術上而言仍然可以評估異質性(如,采用貝葉斯方法),因為異質性評價是系統評價/Meta 分析的基本步驟。針對同一研究問題,當一項研究樣本量非常大且比其他的一個或多個小樣本研究結果更可靠時,選擇 FE 模型[11]。
3.4 研究間異質性
系統評價/Meta 分析中研究間變異性稱為異質性,一般分為臨床異質性(研究對象、干預措施、測量結局等方面的變異性)、方法學異質性(研究設計、測量工具、風險偏倚等方面的變異性)、統計學異質性(不同研究間干預效應方面的變異性),CE 模型沒有考慮異質性,而 FE 模型和 RE 模型均考慮了異質性。系統評價員在解釋結果時必須要考慮統計學異質性,特別是合并效應結果在方向上有變異時[5]。在實踐中,如果要合并的研究間結果異質性非常大,則不宜進行定量合并[8],即不做 Meta 分析[5]。當可以預料到一定程度的異質性、但合并研究的結果重要時,可以用 RE 模型[8]。盡管系統評價員的模型選擇對結果通常影響不大,但當研究結果異質性顯著時,理解模型選擇的原理可以幫助醫師更好地解讀研究結果[11]。
3.5 抽樣框架
一般情況下,應當基于抽樣框架選擇統計模型,因此在選擇模型時應該關注納入 Meta 分析的研究是如何抽樣的,而不是異質性檢驗的統計學結果。在實踐中,在系統評價/Meta 分析的研究中納入的研究人群一般不同來自同一個群體,從邏輯上講,應當選擇 RE 模型來擬合數據。
綜上所述,筆者建議,在制訂系統評價/Meta 分析研究方案時就應該考慮選擇合適的模型,并且要根據研究目的和研究者對適用于數據模型的主觀假設而定。基于 RE 模型的假說和抽樣框架更符合實際、統計推斷目的對研究者而言更有吸引力、從數學角度而言 CE 和 FE 模型是 RE 模型的特例等方面來考慮,除了使用 RE 模型不可能(如只有一個研究)、不合理(異質性參數估計不可靠)等情況外,在 Meta 分析時應首先選用 RE 模型。最后,再次強調《Cochrane 干預措施系統評價員手冊》的重要觀點:決不應該根據異質性統計檢驗做出使用 FE 或 RE 模型的選擇。
4 實例分析
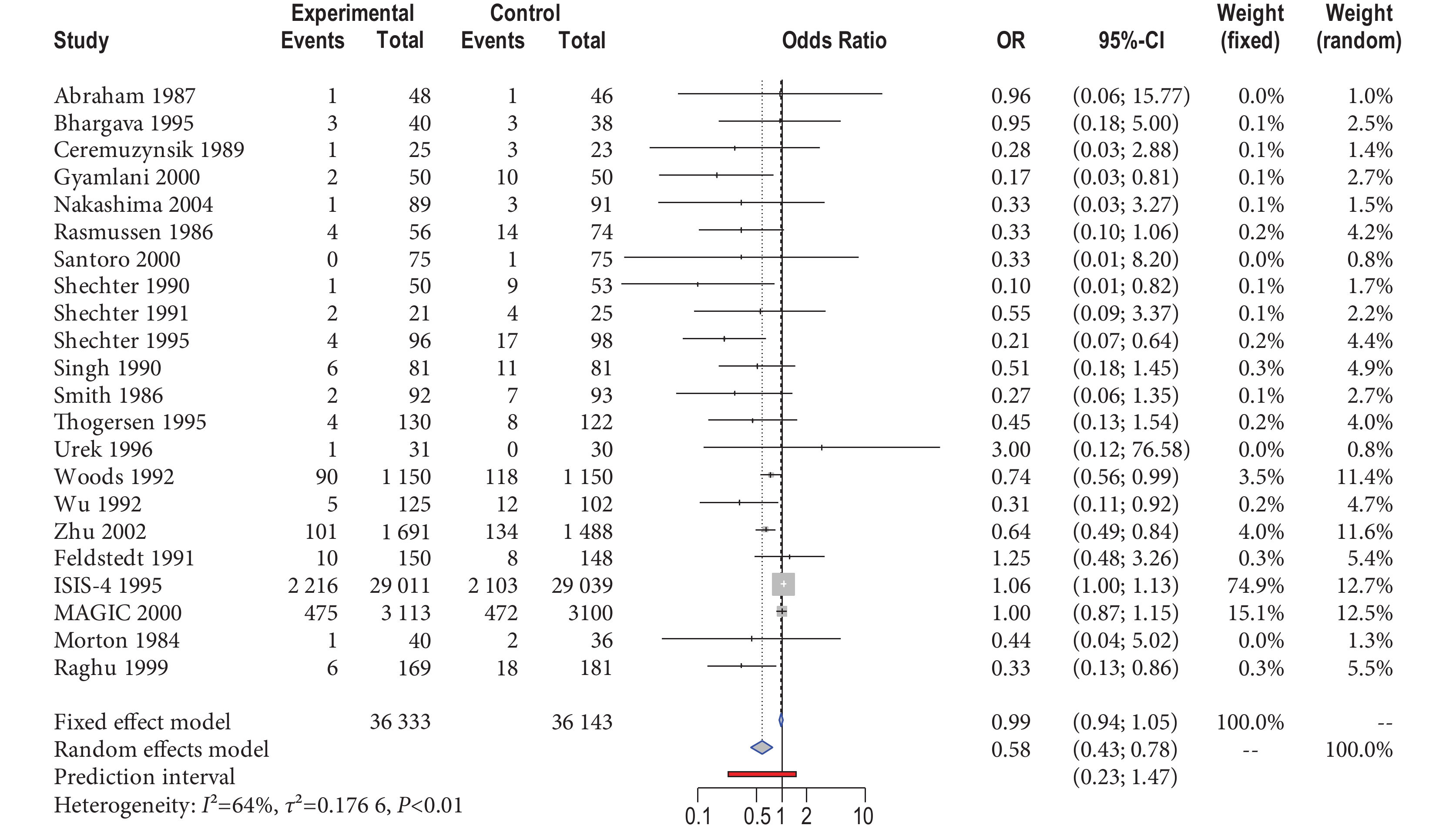
以一個 Cochrane 系統評價[14]為例說明如何選擇和理解經典 Meta 分析中不同效應模型的使用。選取該系統評價中觀察鎂離子對心肌梗死患者死亡率影響的二分類數據,以 R 軟件(ver 4.0.0)中的 meta 擴展包(ver 4.14-0)重新分析,以比值比(odds ratio,OR)為效應量,擬合經典的 FE 和 RE 模型,繪制森林圖如圖 2 所示。主要結果:共納入 22 個研究,具有中度異質性(I2=64%, ),得到 OR 點估計值及 95% 置信區間(confidence interval,CI)分別為 0.99(0.94,1.05)和 0.58(0.43,0.78),兩者結果有明顯的不同。
),得到 OR 點估計值及 95% 置信區間(confidence interval,CI)分別為 0.99(0.94,1.05)和 0.58(0.43,0.78),兩者結果有明顯的不同。
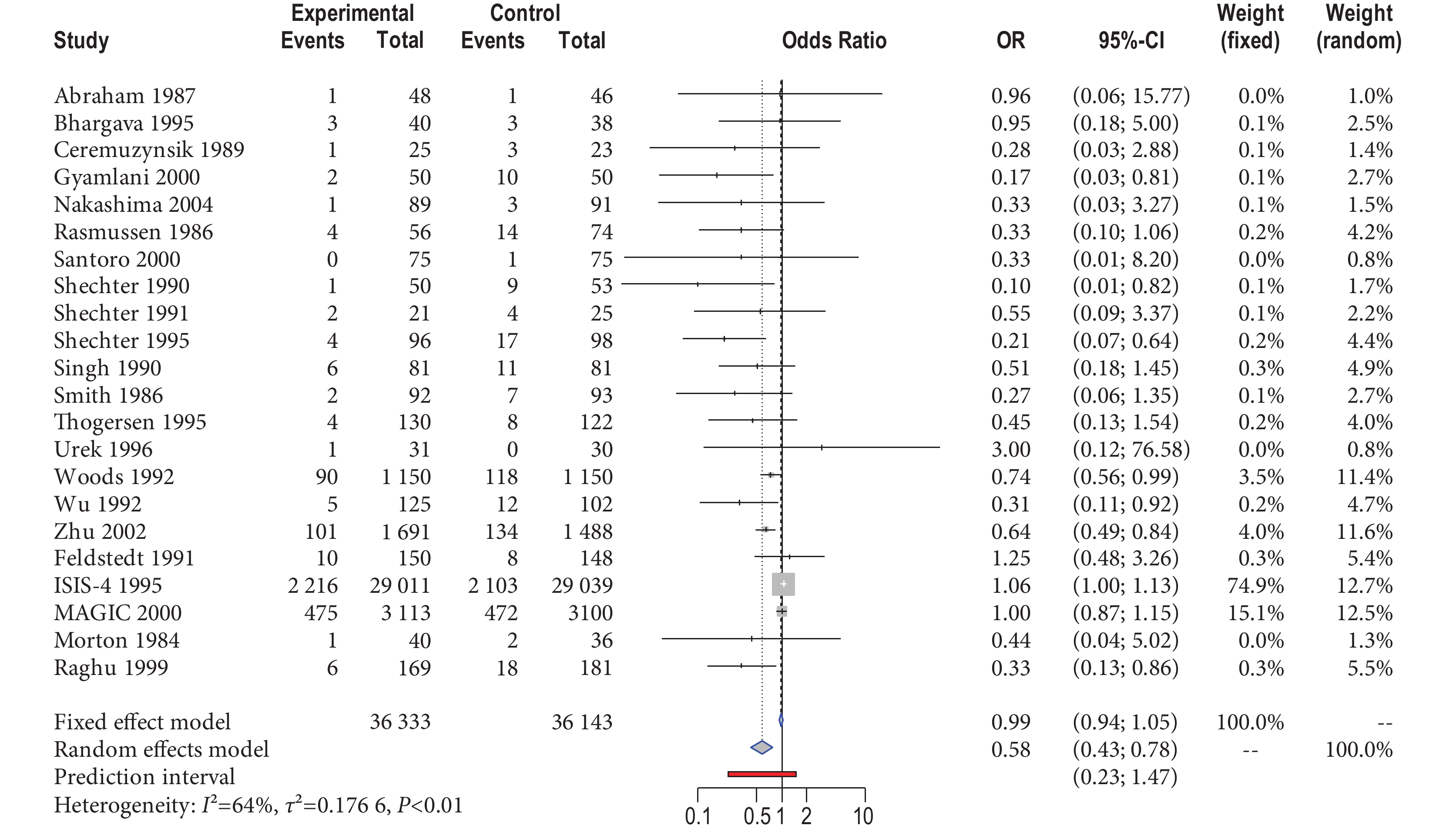 圖2
森林圖
圖2
森林圖
按經典的 FE 和 RE 等“兩模型理論”分析:從圖 2 中可以發現,22 個研究中,大多數研究樣本量較少、但顯示靜脈注射鎂離子明顯降低死亡率(如 Gyamlani 2000、Shechter 1995 等研究);而 ISIS-4 1995、Urek 1996、Felstedt 1991 等研究和其他研究在效應量方向上有明顯不同,顯示靜脈注射鎂離子無獲益。研究間結果差異會降低區間估計值的置信度,可以反映在 RE 模型較寬的 CI 上,似乎選擇 RE 模型更適用。但本數據的情況特殊,即顯示靜脈注射鎂離子無獲益的 2 個研究的樣本量較大,尤其是 ISIS-4 1995 研究的樣本量占到整個系統評價樣本量的 80%,令系統評價員更傾向于相信大樣本研究的結果,從圖 2 中可以發現,FE 模型賦予大樣本研究的權重明顯大于 RE 模型(74.9% vs. 12.7%),說明 FE 模型更重視大樣本研究的結果,因此理論上宜選擇 FE 模型,而實際上該系統評價也是選擇的 FE 模型[14]。如果僅按傳統方法基于異質性檢驗結果來選擇效應模型,則會因存在異質性而選擇 RE 模型,可能令臨床證據使用者和衛生政策決策者陷入誤區。
按新近的 CE、FE 和 RE“三模型理論”分析:基于模型假設和研究目的等方面考慮選擇合適的模型。① CE 模型假定納入 Meta 分析中所有研究的效應量均相同,且等于真實值,研究目的在于估計共同的效應量(真實值),但從圖 2 中可發現,該假設難以成立,不建議選擇。② FE 模型允許研究的效應量不同,但總體參數是固定數量,研究目的在于觀察納入 Meta 分析各研究的效應量平均值。如果納入 Meta 分析中不同研究的真實效應不同而研究目的僅是對納入 Meta 分析研究的效應量平均值感興趣,并進行推斷,則可選擇 FE 模型。因此,本例選擇 FE 模型較為合理。③ RE 模型認為,納入 Meta 分析的研究效應量不同,而且納入的研究只是從更大的研究群體中抽樣,因此 RE 模型的研究目的是基于抽樣的研究推斷總體研究,推斷目標總體參數(真實值)是各研究量效應量分布的均數,如本例中納入 Meta 分析各研究的效應量(各個研究的 lnOR)是來自均數為?0.54、標準差為 0.15 的正態分布,如圖 3 所示。雖然系統評價員有 95% 的信心認為在(?0.84,?0.25)區間包含真實值(OR 對數尺度),但是不能確定由本次系統評價 22 個研究所構造的 95%CI 是否真的包含真實值。在經典統計學中,參數是固定的但未知,因此一個特定的區間總是包含或是絕對不包含真實值[15],而實際上 ISIS-4 1995、Felstedt 1991 這兩個大樣本研究的效應量(lnOR)遠離均數值,且在 95%CI 區域外,提示我們效應量真實值可能在 95%CI 之外。
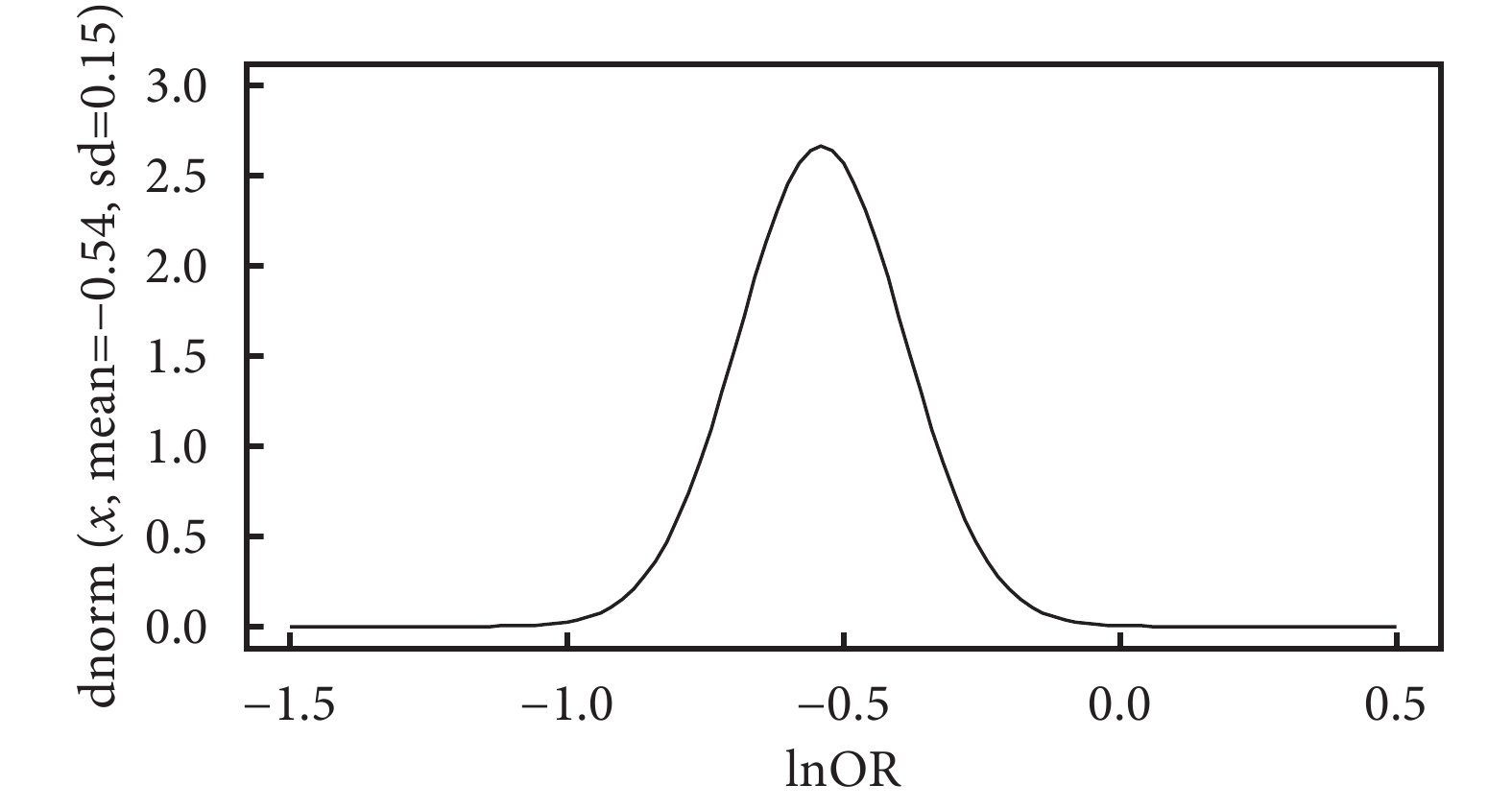 圖3
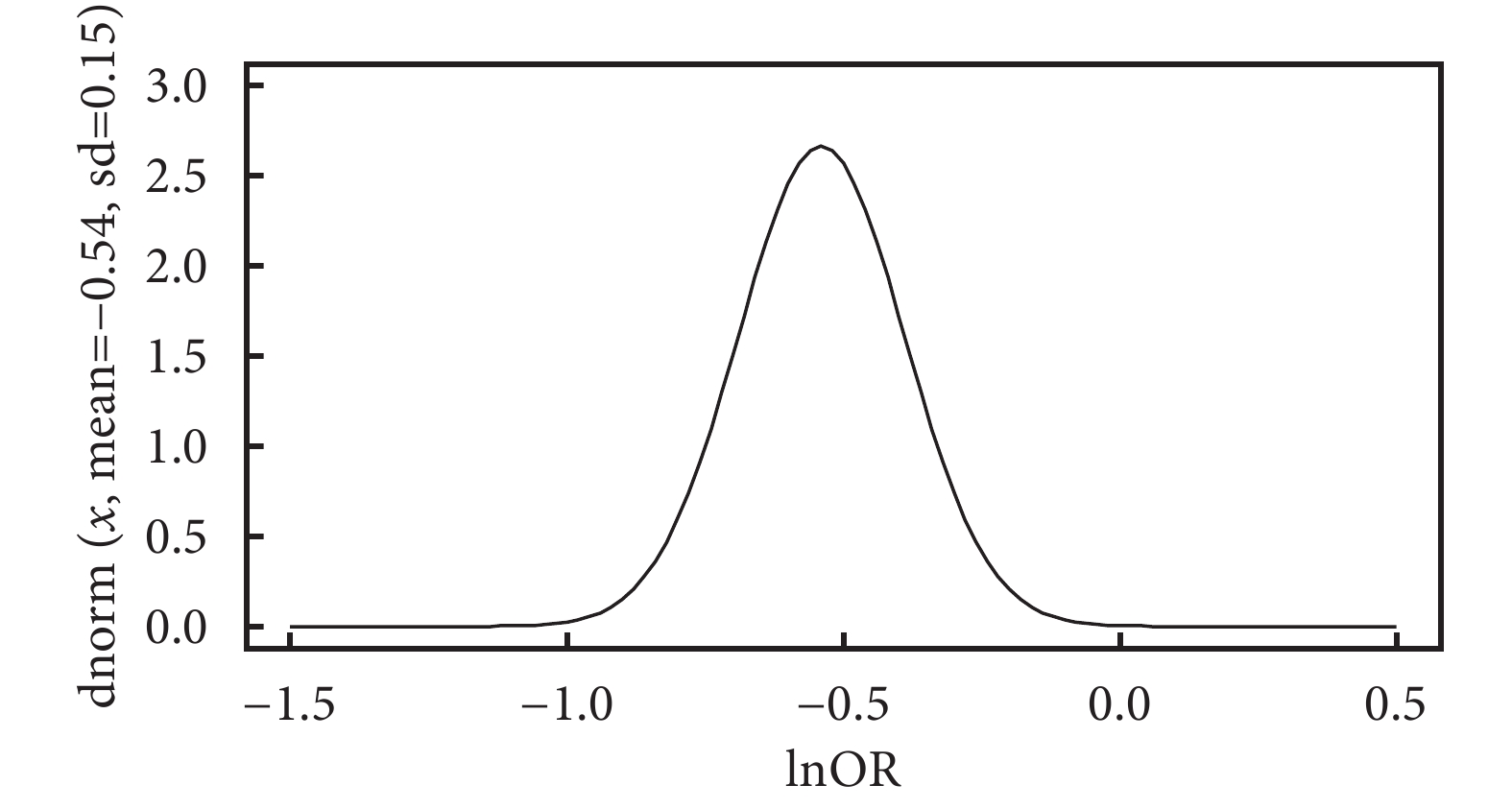
各研究效應量(OR 對數尺度)分布曲線
圖3
各研究效應量(OR 對數尺度)分布曲線
Meta 分析可定量、科學地整合研究結果,已在許多科學領域取得顯著成果[1]。在醫學領域常可用于比較不同干預措施有益還是有害[2]。一般認為,經典 Meta 分析合并數據最主要的統計模型是固定效應(fixed-effect,FE)模型和隨機效應(random-effect,RE)模型[3, 4]。合理選擇 Meta 分析合并模型非常重要,在 Meta 分析實踐中,一些研究者首先選用 FE 模型,然后進行效應量的異質性檢驗(如,Q 統計量),若異質性檢驗無統計學意義,則認為 FE 模型適合于數據,宜采用 FE 模型分析;若異質性檢驗有統計學意義,則認為 FE 模型不適合于數據,宜采用 RE 模型分析[3]。但這類應當避免的模型選擇錯誤可影響整合研究結果的準確性,在第 6 版《Cochrane 干預措施系統評價員手冊》[5]明確指出:“決不應該根據異質性統計檢驗做出使用 FE 或 RE 模型的選擇”。因此,本文在復習文獻基礎上,介紹經典 Meta 分析統計模型的新觀點及其假設、結果解釋,探討合理選擇模型時應考慮的因素,以及如何合理選擇應用。
1 Meta 分析的基本原理
經典 Meta 分析是典型的二步過程,其基本原理是[5]:第一步,計算納入 Meta 分析的每個研究的統計量。用相同方法來描述每個研究干預的觀測效應量。第二步,通過對每個研究干預的觀測效應量進行加權取平均數來獲得總的合并干預效應。其公式為:
 |
式中, 為第 i 個研究中的干預效應(如,比值比對數、相對危險比對數、風險比對數、率差、均數差、標化均數差等效應量),
為第 i 個研究中的干預效應(如,比值比對數、相對危險比對數、風險比對數、率差、均數差、標化均數差等效應量), 為第 i 個研究的權重。
為第 i 個研究的權重。
從公式(1)可知,如果每個研究的權重相同,則加權平均數等于干預效應的平均值。
2 Meta 分析統計模型及其假設與解釋
經典 Meta 分析的統計模型對于計算和解釋 Meta 分析的結果非常重要,但由于 FE 和 RE 統計模型采用相似的公式計算統計量,有時可能得到相似的結果,以至常被誤認為兩個模型可相互替換使用。但實際上,不同模型基于不同假設,并且提供不同的參數估計值。
FE 模型[4, 6, 7]假設納入 Meta 分析的所有研究均有一個相同的干預效應(量級和方向均相同),不同研究的觀測效應量之間的差異均由抽樣誤差所示(如圖 1 左側部分所示)。合并效應量是研究特定效應量的加權平均數;每個研究分配到的權重等于研究內效應量方差的倒數;大樣本研究所占權重大幅度高于小樣本研究;研究的精度越大,對合并效應量的貢獻度就越大;故統計推斷有可能受到納入分析的樣本量影響。
 圖1
固定效應模型和隨機效應模型圖解(引自 Nikolakopoulou 等[6]的文獻)
圖1
固定效應模型和隨機效應模型圖解(引自 Nikolakopoulou 等[6]的文獻)
RE 模型[4, 6, 7]假設納入分析的研究間干預效應可以不同,觀測效應量的不同由隨機誤差和真實干預效應不同所致(圖 1 右則部分所示)。合并效應量是研究特定效應量的加權平均數;每個研究分配到的權重等于研究內效應量方差與研究間異質性方差和的倒數;大樣本研究占權重高于小樣本研究,但大樣本研究所占權重比在 FE 模型中小;對未來研究干預效應的預測更可靠;預測區間可表達真實效應量離散程度,可用于解釋單個研究真實效應量的預測范圍。
Bender[8]、Rice[9]等根據研究目的和假設等將 Meta 分析統計模型拓展為三個:共同效應(common-effect,CE)模型、FE模型和 RE 模型,請注意此處的 FE 模型與經典“FE 模型”的英文表達方式不同,在最新版 Stata 16.0 軟件中關于 Meta 分析的統計模塊采用的是這三種模型[10]。假設納入分析的第  (
( )個研究的觀測效應量為
)個研究的觀測效應量為  ,其相應方差為
,其相應方差為  ,真實效應量為
,真實效應量為  ,研究間異質性方差為
,研究間異質性方差為  ;描述第 i 個研究的抽樣誤誤差的隨機變量為
;描述第 i 個研究的抽樣誤誤差的隨機變量為  ,描述研究間異質性的隨機變量為
,描述研究間異質性的隨機變量為  ,合并效應量為
,合并效應量為  ,則三個模型的表達、假設、結果解釋等比較如表 1 所示,從中可以看出,Bender 等提出的 CE 模型和 FE 模型使用的加權平均統計量相同,因此所獲得的結果也相同。
,則三個模型的表達、假設、結果解釋等比較如表 1 所示,從中可以看出,Bender 等提出的 CE 模型和 FE 模型使用的加權平均統計量相同,因此所獲得的結果也相同。
3 不同模型的合理選擇依據和建議
Meta 分析中如何選擇統計模型,歷來存有爭議。不同的統計學家和臨床研究人員可能偏愛不同的統計模型[11],即使是第 6 版《Cochrane 干預措施系統評價員手冊》也未能提供權威的統一推薦意見[5]。筆者認為,應從統計模型假說、Meta 分析目的、納入 Meta 分析的研究數量和樣本量、研究間異質性、抽樣框架等不同方面綜合考慮來選擇合適的統計模型。
3.1 統計模型假說
如果假定納入 Meta 分析的研究具有共同的效應量,則可選用 CM 模型,但一般認為跨研究間干預效應完全相同是難以置信的(除非干預毫無效果)[5],這也是 CM 模型最主要的局限[8]。如果假定研究具有不同的干預效應,但效應量是“固定的”,則可選用 FE 模型;如果效應量是“隨機的”,則可選用 RE 模型。
3.2 Meta 分析目的
如果研究者的意圖僅僅是獲得納入 Meta 分析研究的干預效應平均值,則選用 FE 模型;如果研究意圖不僅僅是獲得納入 Meta 分析研究的干預效應平均值,而是要了解推廣應用到更為廣泛的人群的效應,則可選用 RE 模型[11, 12]。
3.3 研究數量和樣本量
納入 Meta 分析的研究數量足夠多時選擇 RE 模型,數量少時宜選擇 FE 模型[12]。雖然 RE 模型通常情況下是合適的模型,但當研究數量非常少( )時,因難以準確估計研究間方差,宜選擇 FE 模型[3, 11, 13]。特別是,當研究數量
)時,因難以準確估計研究間方差,宜選擇 FE 模型[3, 11, 13]。特別是,當研究數量  時,采用 CE 模型或 FE 模型,但更傾向于選擇 CE 模型,除非有違背 CE 模型假設的強假設[8]。但需要指出的是,即使是研究數量少(k=2~4)時,從技術上而言仍然可以評估異質性(如,采用貝葉斯方法),因為異質性評價是系統評價/Meta 分析的基本步驟。針對同一研究問題,當一項研究樣本量非常大且比其他的一個或多個小樣本研究結果更可靠時,選擇 FE 模型[11]。
時,采用 CE 模型或 FE 模型,但更傾向于選擇 CE 模型,除非有違背 CE 模型假設的強假設[8]。但需要指出的是,即使是研究數量少(k=2~4)時,從技術上而言仍然可以評估異質性(如,采用貝葉斯方法),因為異質性評價是系統評價/Meta 分析的基本步驟。針對同一研究問題,當一項研究樣本量非常大且比其他的一個或多個小樣本研究結果更可靠時,選擇 FE 模型[11]。
3.4 研究間異質性
系統評價/Meta 分析中研究間變異性稱為異質性,一般分為臨床異質性(研究對象、干預措施、測量結局等方面的變異性)、方法學異質性(研究設計、測量工具、風險偏倚等方面的變異性)、統計學異質性(不同研究間干預效應方面的變異性),CE 模型沒有考慮異質性,而 FE 模型和 RE 模型均考慮了異質性。系統評價員在解釋結果時必須要考慮統計學異質性,特別是合并效應結果在方向上有變異時[5]。在實踐中,如果要合并的研究間結果異質性非常大,則不宜進行定量合并[8],即不做 Meta 分析[5]。當可以預料到一定程度的異質性、但合并研究的結果重要時,可以用 RE 模型[8]。盡管系統評價員的模型選擇對結果通常影響不大,但當研究結果異質性顯著時,理解模型選擇的原理可以幫助醫師更好地解讀研究結果[11]。
3.5 抽樣框架
一般情況下,應當基于抽樣框架選擇統計模型,因此在選擇模型時應該關注納入 Meta 分析的研究是如何抽樣的,而不是異質性檢驗的統計學結果。在實踐中,在系統評價/Meta 分析的研究中納入的研究人群一般不同來自同一個群體,從邏輯上講,應當選擇 RE 模型來擬合數據。
綜上所述,筆者建議,在制訂系統評價/Meta 分析研究方案時就應該考慮選擇合適的模型,并且要根據研究目的和研究者對適用于數據模型的主觀假設而定。基于 RE 模型的假說和抽樣框架更符合實際、統計推斷目的對研究者而言更有吸引力、從數學角度而言 CE 和 FE 模型是 RE 模型的特例等方面來考慮,除了使用 RE 模型不可能(如只有一個研究)、不合理(異質性參數估計不可靠)等情況外,在 Meta 分析時應首先選用 RE 模型。最后,再次強調《Cochrane 干預措施系統評價員手冊》的重要觀點:決不應該根據異質性統計檢驗做出使用 FE 或 RE 模型的選擇。
4 實例分析
以一個 Cochrane 系統評價[14]為例說明如何選擇和理解經典 Meta 分析中不同效應模型的使用。選取該系統評價中觀察鎂離子對心肌梗死患者死亡率影響的二分類數據,以 R 軟件(ver 4.0.0)中的 meta 擴展包(ver 4.14-0)重新分析,以比值比(odds ratio,OR)為效應量,擬合經典的 FE 和 RE 模型,繪制森林圖如圖 2 所示。主要結果:共納入 22 個研究,具有中度異質性(I2=64%, ),得到 OR 點估計值及 95% 置信區間(confidence interval,CI)分別為 0.99(0.94,1.05)和 0.58(0.43,0.78),兩者結果有明顯的不同。
),得到 OR 點估計值及 95% 置信區間(confidence interval,CI)分別為 0.99(0.94,1.05)和 0.58(0.43,0.78),兩者結果有明顯的不同。
 圖2
森林圖
圖2
森林圖
按經典的 FE 和 RE 等“兩模型理論”分析:從圖 2 中可以發現,22 個研究中,大多數研究樣本量較少、但顯示靜脈注射鎂離子明顯降低死亡率(如 Gyamlani 2000、Shechter 1995 等研究);而 ISIS-4 1995、Urek 1996、Felstedt 1991 等研究和其他研究在效應量方向上有明顯不同,顯示靜脈注射鎂離子無獲益。研究間結果差異會降低區間估計值的置信度,可以反映在 RE 模型較寬的 CI 上,似乎選擇 RE 模型更適用。但本數據的情況特殊,即顯示靜脈注射鎂離子無獲益的 2 個研究的樣本量較大,尤其是 ISIS-4 1995 研究的樣本量占到整個系統評價樣本量的 80%,令系統評價員更傾向于相信大樣本研究的結果,從圖 2 中可以發現,FE 模型賦予大樣本研究的權重明顯大于 RE 模型(74.9% vs. 12.7%),說明 FE 模型更重視大樣本研究的結果,因此理論上宜選擇 FE 模型,而實際上該系統評價也是選擇的 FE 模型[14]。如果僅按傳統方法基于異質性檢驗結果來選擇效應模型,則會因存在異質性而選擇 RE 模型,可能令臨床證據使用者和衛生政策決策者陷入誤區。
按新近的 CE、FE 和 RE“三模型理論”分析:基于模型假設和研究目的等方面考慮選擇合適的模型。① CE 模型假定納入 Meta 分析中所有研究的效應量均相同,且等于真實值,研究目的在于估計共同的效應量(真實值),但從圖 2 中可發現,該假設難以成立,不建議選擇。② FE 模型允許研究的效應量不同,但總體參數是固定數量,研究目的在于觀察納入 Meta 分析各研究的效應量平均值。如果納入 Meta 分析中不同研究的真實效應不同而研究目的僅是對納入 Meta 分析研究的效應量平均值感興趣,并進行推斷,則可選擇 FE 模型。因此,本例選擇 FE 模型較為合理。③ RE 模型認為,納入 Meta 分析的研究效應量不同,而且納入的研究只是從更大的研究群體中抽樣,因此 RE 模型的研究目的是基于抽樣的研究推斷總體研究,推斷目標總體參數(真實值)是各研究量效應量分布的均數,如本例中納入 Meta 分析各研究的效應量(各個研究的 lnOR)是來自均數為?0.54、標準差為 0.15 的正態分布,如圖 3 所示。雖然系統評價員有 95% 的信心認為在(?0.84,?0.25)區間包含真實值(OR 對數尺度),但是不能確定由本次系統評價 22 個研究所構造的 95%CI 是否真的包含真實值。在經典統計學中,參數是固定的但未知,因此一個特定的區間總是包含或是絕對不包含真實值[15],而實際上 ISIS-4 1995、Felstedt 1991 這兩個大樣本研究的效應量(lnOR)遠離均數值,且在 95%CI 區域外,提示我們效應量真實值可能在 95%CI 之外。
 圖3
各研究效應量(OR 對數尺度)分布曲線
圖3
各研究效應量(OR 對數尺度)分布曲線